Question

Assertion: The equation \[x\ln x=2-x\] is satisfied by at least one value of x lying between 1 and 2
Reason: The function \[f\left( x \right)=x\ln x\] is an increasing function in [1, 2] and the graph represented by these functions intersected at a point in [1, 2].
(a) Both Assertion and Reason are correct and Reason is the correct explanation for Assertion
(b) Both Assertion and Reason are correct and Reason is not the correct explanation for Assertion
(c) Assertion is correct but Reason is incorrect
(d) Both Assertion and Reason are incorrect

Answer 1

Hint: To solve the given question, we will first find out what an increasing function is and how it is related to the derivative of that function. Then we will assume that \[f\left( x \right)=x\ln x\] and \[g\left( x \right)=2-x.\] Then we will check the behaviour of both f(x) and g(x) in [1, 2]. We will find their extreme values in [1, 2]. Then we will see the behaviour of their derivatives in [1, 2]. On the basis of this we will draw rough graphs of f(x) and g(x) in the domain [1, 2] and check whether they have intersection points or not. On the basis of all these, we will choose the correct option.

Complete step by step solution:
Before we solve the given question, we must know what increasing and decreasing functions are. Increasing functions are those functions whose value increases when we increase the value of independent variables. Decreasing functions are those functions whose value decreases when we increase the value of the independent variable. For function to be increasing, the first derivative of the function with respect to the independent variable should be positive.
Now, we assume that \[x\ln x=f\left( x \right)\] and \[2-x=g\left( x \right).\] Now, we have to find their behaviour in [1, 2]. Let us first find the values of f(x) at endpoints. The value of f(1) is:
\[f\left( 1 \right)=1\ln \left( 1 \right)=0\]
Similarly, \[f\left( 2 \right)=2\ln \left( 2 \right)=2\times 0.69=1.38\]
Now, we will find the values of g(x) at end points. The value of g(1) = 2 – 1 = 1. Similarly, g(2) = 2 – 2 = 0.
Now, let us find the behaviour of their derivatives. The derivative of f(x) is given by
\[\dfrac{d}{dx}\left( f\left( x \right) \right)=\dfrac{d}{dx}\left[ x\ln x \right]\]
For differentiation, we will use the product rule. According to the product rule,
\[\dfrac{d}{dx}\left( a.b \right)=b\dfrac{da}{dx}+a\dfrac{db}{dx}\]
Thus, we will get,
\[{{f}^{'}}\left( x \right)=\ln x\dfrac{dx}{dx}+x\dfrac{d}{dx}\left( \ln x \right)\]
\[\Rightarrow {{f}^{'}}\left( x \right)=\ln x\left( 1 \right)+\dfrac{x}{x}\]
\[\Rightarrow {{f}^{'}}\left( x \right)=\ln x+1\]
Now, \[{{f}^{'}}\left( 1 \right)=\ln \left( 1 \right)+1=1\]
Similarly,
\[{{f}^{'}}\left( 2 \right)=\ln \left( 2 \right)+1=1+0.693=1.693\]
Thus, f’(x) is positive in [1, 2]. Thus, f(x) is an increasing function in [1, 2].
Now, the derivative of g(x) will be
\[\dfrac{d}{dx}\left( g\left( x \right) \right)=\dfrac{d}{dx}\left[ 2-x \right]\]
\[\Rightarrow {{g}^{'}}\left( x \right)=-1\]
Now, g’(x) is always negative, thus, g(x) is a decreasing function. Now, we will draw rough graphs of f(x) and g(x) on the basis of our above findings.

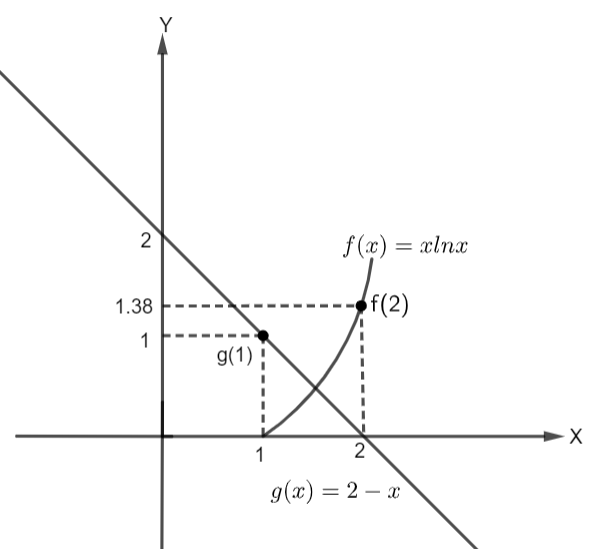
Thus, we can see that f(x) and g(x) intersects between x = 1 and x = 2. This means that our assertion is true. Now, the reason will also be true as f(x) is an increasing function in [1, 2]. Now, due to f(x) being an increasing function, there will be an intersection point.
Hence, we can say that the reason is the correct explanation for assertion.
Hence, option (a) is the right answer.

Note: The solution of equation \[x\ln x=2-x\] can also be determined by the following method
\[x\ln x=2-x\]
\[\Rightarrow x\ln x+x=2\]
\[\Rightarrow x\left( \ln x+1 \right)=2\]
Now, we can write 1 as ln e. Thus,
\[\Rightarrow x\left( \ln x+\ln e \right)=2\]
\[\Rightarrow x\left( \ln ex \right)=2\]
\[\Rightarrow x\ln ex=2\]
Now, \[x\ln ex\] is an increasing function and is also continuous. At x= 1, its value is 0. At x = 2, its value is 3.386. Thus, we can say that between x = 1 and x = 2, there will be at least one value of x where the value of \[x\ln ex\] will be 2. Thus, it has one solution.