Question

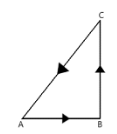
As shown in figure, on bringing a charge Q from point A to B and from point B to C, the work done are 2 Joules and -3 Joules respectively. The work done in bringing the charge from C to A will be:

(A) -1 Joule
(B) 1 Joule
(C) 2 Joules
(D) 5 Joule

Answer 1

Hint The work done in moving a charge in an electric field from one place to another is independent of path taken i.e. only depends on the start and end point. Also, the work done in moving a charge from a point X to point Y is equal but opposite in sign to the work done in moving from point Y to point X. So from this we can calculate the value of the work done from C to A.

Complete step by step answer
In physics, there's a classification of forces called conservative forces. An electric field is a conservative force.
In general, conservative forces are forces with a property such that the work done in moving from a point to another is entirely independent of the path taken to travel between the points. It can also be defined as forces with properties such that the work done in a complete loop, is zero. i.e. the work done in going between two points, to and fro is zero. This is because when work is done in the direction of the force, it is considered positive, but when work is done opposite the direction of the force, it is considered negative. The total work done is the sum of the work done on each path.
Now, in the question, work done from A to B is 2 J i.e.
 $\Rightarrow W_{AB}=2\text{J}$
Work done from B to C is -3 J i.e.
 $\Rightarrow W_{AB}=-3\text{J}$
The total work done from A to C through path ABC is thus
 $\Rightarrow W_{ABC}=2+\left(-3\right)\text{ = }-1\text{J}$
Now, since work done is independent of path taken, then, work done from A to C directly is also -1 J. Hence $W_{AC}=-1\text{J}$
Also, work done from A to C is also equal to work done from C to A, but opposite in sign. Hence,
 $\Rightarrow W_{CA}=+1\text{J}$ where $W_{CA}$ is work done from C to A.
Hence, the correct option is B.

Note
Alternatively, since the work done around a closed loop is zero, then
 $\Rightarrow W_{AB}+W_{BC}+W_{CA}=0$
Hence, inserting known values we have
 $\Rightarrow +2+\left(-3\right)+W_{CA}=0$
 $\Rightarrow -1+W_{CA}=0$
Hence, $W_{CA}=1\text{J}$ .