Question

As shown in figure, a spherical air lens of radii R1=R2=10cm, is cut in a glass $(\mu =1.5)$cylinder. Determine the focal length and nature of the air lens. If liquid of refractive index 2 is filled in the lens, find its focal length and nature.

Answer 1

Hint: Speed of light is constant in vacuum, but when it enters in a different medium due to the refractive index of that medium speed changes and reflects or refracts according to the medium and refractive index varies from medium to medium. To solve our problem first we will find focal length normally than we will calculate after the lens was filled with liquid.

Formula used:
$\dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$

Complete Step by step solution:
In our first case, by assuming the lens is filled with air (refractive index=1) and for the surrounding medium (glass) refractive index is 1.5.

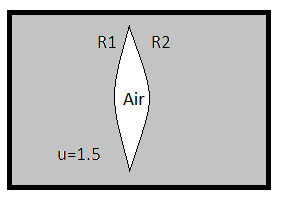
Now by using lens maker formula we have,
$\dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$

Here, $f$ (focal length to be calculated, $\mu $ (refractive index with respect to surrounding medium $\mu =\dfrac{{{\mu }_{l}}}{{{\mu }_{m}}}$ ${{\mu }_{l}}$is refractive index of lens and ${{\mu }_{m}}$ is refractive index of medium) and ${{R}_{1}}$and${{R}_{2}}$(radius of curvatures).

Now, ${{R}_{1}}$=10 cm and ${{R}_{2}}$=-10 cm (opposite direction)
So, by applying the above formula we have,
$\Rightarrow \dfrac{1}{f}=(\dfrac{1}{1.5}-1)\left[ \dfrac{1}{10}-\dfrac{1}{(-10)} \right]$,
$\Rightarrow \dfrac{1}{f}=(\dfrac{2}{3}-1)\left[ \dfrac{1}{10}+\dfrac{1}{10} \right]$,
$\Rightarrow \dfrac{1}{f}=(-\dfrac{1}{3})\left[ \dfrac{2}{10} \right]$,
$\Rightarrow \dfrac{1}{f}=-\dfrac{2}{30}=-\dfrac{1}{15}$
So, $f=-15cm$

$\Rightarrow $ The value of focal length is negative so we can say that an air lens in glass will be behaving as a diverging lens with a focal length of 15 cm.

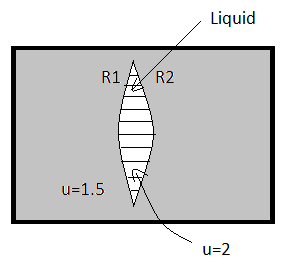
Now, after filling the lens with liquid of refractive index 2 equivalent refractive index will be,
$\mu =\dfrac{{{\mu }_{l}}}{{{\mu }_{m}}}=\dfrac{2}{1.5}=\dfrac{4}{3}$

By applying lens maker formula we have,
$\Rightarrow \dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$
$\Rightarrow \dfrac{1}{f}=(\dfrac{4}{3}-1)\left[ \dfrac{1}{10}-\dfrac{1}{(-10)} \right]$,
$\Rightarrow \dfrac{1}{f}=(\dfrac{1}{3})\left[ \dfrac{1}{10}+\dfrac{1}{10} \right]$
$\Rightarrow \dfrac{1}{f}=(\dfrac{1}{3})\left[ \dfrac{2}{10} \right]=\dfrac{1}{15}$
$f=15cm$

$\Rightarrow$ After filling with liquid focal length was changed to 15 cm (positive) lens will be behaving as a converging lens with focal length of 15 cm.

Note:
In the above solution we can see that before and after filling the liquid inside the lens the nature of the lens is changed from divergent to convergent of focal length 15 cm. In the ideal condition (vacuum) we don’t need to add a refractive index in consideration because there will be no medium change so the nature of the lens will not be affected.