Question

Any chord of the conic ${{x}^{2}}+{{y}^{2}}+xy=1$ passing through the origin is bisected at a point$(p,q)$ then $(p+q+12)$ equals to :
(a) 13
(b) 14
(c) 11
(d) 12

Answer 1

Hint: Make use of the property that says that the centre of a conic bisects every chord that passes through the centre of a conic section.

First, let’s find the centre of this conic section. To find this, let’s first see if the equation changes when we replace $x$ with $y$ and vice versa. If the equation remains unchanged, then that means that the centre of the conic is the origin itself.
Let’s exchange $x$ and $y$ in the equation now. Doing so, we get :
${{y}^{2}}+{{x}^{2}}+yx=1$ which is the same as the original question.
Hence, we know that the centre of this conic is in fact the origin.
It is a property of all conics that every chord drawn in the conic that passes through its centre is bisected by the centre of that conic. Applying this property to this question, since we don’t have one particular chord, and it’s any chord passing through the origin, we can say that $(p,q)$ is actually the centre of this conic. Hence, this point should be equal to the origin since that is the centre of this conic.
$\begin{align}
  & (p,q)=(0,0) \\
 & \Rightarrow p=0,q=0 \\
 & \Rightarrow p+q+12=0+0+12=12 \\
\end{align}$
Hence, $(p+q+12)=12$ in this question.
Note:

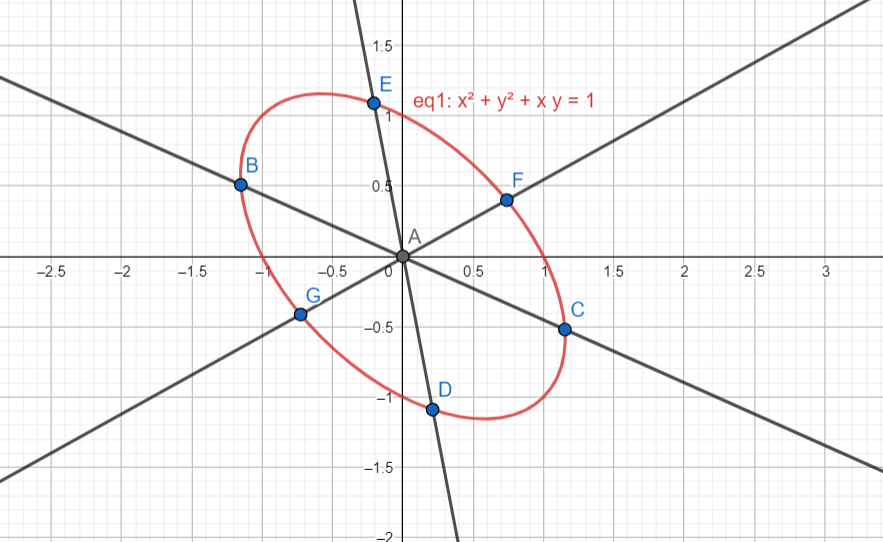
Here, A is the centre of the conic, the origin, and as you can see, it bisects every chord that passes through it.