Question

Answer the following questions:
i. Define electric flux. Write its SI units.
ii. Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
iii. How is the field directed if (i) the sheet is positively charged, (ii) negatively charged?

Answer 1

Hint: The electric flux through a given area held inside an electric field is the measure of the total number of electric lines of force passing through that area. Mathematically, it can be defined as the product of the normal component of the electric field and the surface area. Using its mathematical expression we can find the electric field at any point near any physical shape.
Formula Used:
Electric flux, ${\phi _E} = \dfrac{q}{{{\varepsilon _ \circ }}}$
where
$\eqalign{
  & {\text{q is the charge enclosed by the closed surface}} \cr
  & {\varepsilon _ \circ }{\text{ is the permittivity of free space}} \cr} $

Complete step by step answer:
The term flux implies some kind of flow. Flux is the property of any vector field. The electric flux is a property of the electric field. The electric flux through a given area held inside an electric field is the measure of the total number of electric lines of force passing through that area.

It is a scalar quantity, i.e., it only has magnitude associated with it and not direction. Its SI unit is$N{m^2}{C^{ - 1}}$.

Gauss’s theorem is used to give a relation between the total flux passing through any closed surface and the net charge enclosed by this surface. It states that the total electric flux through a closed surface is $\dfrac{1}{{{\varepsilon _ \circ }}}$ times the net charge enclosed by this closed surface.

Mathematically,
${\phi _E} = \oint\limits_S {\vec E.d\vec S = \dfrac{q}{{{\varepsilon _ \circ }}}} $

Consider a thin, infinite plane sheet of charge having uniform surface charge density $\sigma $ .
We wish to find the electric field at a point P at distance r from this sheet.

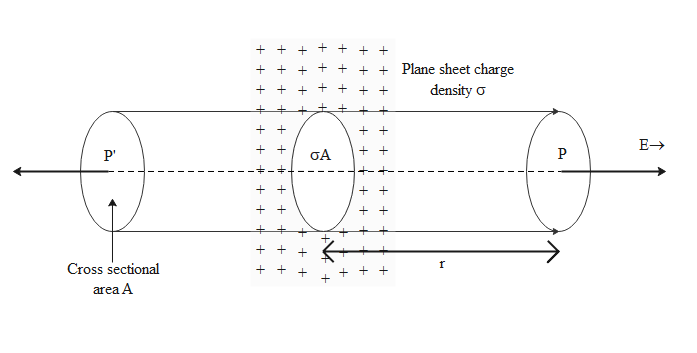
By symmetry, electric field E must point outwards normal to the uniform plane sheet. Also, it must have the same magnitude and opposite direction at two points P and P’ equidistant from the sheet and on opposite sides.

We choose a cylindrical Gaussian surface of cross-sectional area A and length 2r with its axis perpendicular to the sheet. Because the lines of force are parallel to the curved surface of the cylinder, thus the flux through the curved surface is equal to zero. The flux through the plane-end faces of the cylinder is given by:
$\eqalign{
  & {\phi _E} = EA + EA \cr
  & {\phi _E} = 2EA \cr} $

Charge enclosed by three Gaussian surface,
$q = \sigma A$
According to Gauss’s theorem,
$\eqalign{
  & {\phi _E} = \dfrac{q}{{{\varepsilon _ \circ }}} \cr
  & \Rightarrow 2EA = \dfrac{{\sigma A}}{{{\varepsilon _ \circ }}} \cr
  & \therefore E = \dfrac{\sigma }{{2{\varepsilon _ \circ }}} \cr} $
Clearly, E is independent of r, the distance from the plane sheet.

(i) If the sheet is positively charged i.e., $\sigma > 0$the field is directed away from it.
(ii) If the sheet is negatively charged i.e., $\sigma < 0$the field is directed towards it.

Note: The electric field appearing in the Gauss’s theorem is due to all the charges, both inside and outside the closed surface. However, the charge q appearing in the theorem is only contained within the closed surface. Gauss’s law is based on the inverse square dependence on the distance contained in Coulomb's law.