Question

An open box is made of wood 3 cm thick. Its external length, breadth and height are 1.48m, 1.6m and 8.3 cm. Find the cost of painting the inner surface at Rs 50 per sq. meter.
(a) Rs 279.70
(b) Rs 270.10
(c) Rs 219.70
(d) Rs 179.70

Answer 1

Hint: Calculate the internal dimensions of the box using its external dimensions and its thickness. Then calculate the total surface area of the box using its internal dimensions. Finally multiply the obtained total area with the rate of cost of painting to get the answer.

Complete step-by-step answer:
According to the question, we have to find the cost of painting the inner surface. For this we need to find the surface area of the inner side.
From the given information about the box:
External length = 1.48 m
External breadth= 1.16m
External height=8.3dm =0.83m
Width of the box=3cm=0.03m
Let’s see the diagrams for better visualization:

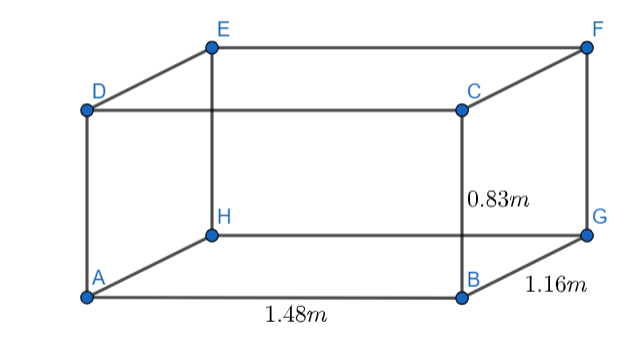
This diagram is the isometric view. Let’s consider the top view also:

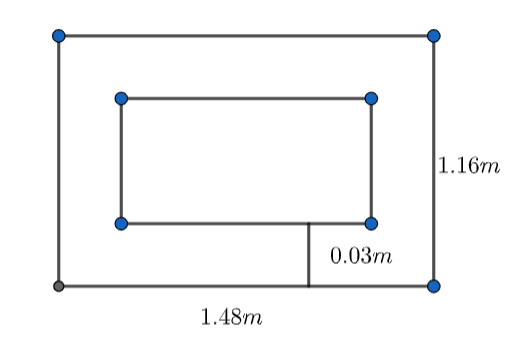
From the top view, we can see that: internal dimension=external dimension – 2 $\times $ thickness.
So, internal length= external length - 2 $\times $ thickness.
$\begin{align}
  & \Rightarrow \operatorname{int}ernal\,length=1.48m-2\left( 0.03 \right)m \\
 & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=1.48m-0.06m \\
 & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=1.42m \\
\end{align}$
Similarly, internal breadth = external breadth – 2 $\times $ thickness.
  $\begin{align}
  & =1.16m-2\left( 0.03 \right) \\
 & =1.16m-0.06m \\
 & =1.10m \\
\end{align}$
For internal height, the box is open. So, internal height = external height - thickness.
$\begin{align}
  & =0.83m-0.03m \\
 & =0.80m \\
\end{align}$
Now, we have got the internal dimension of the box. We have to find the internal surface area.
We know that area of four walls= $2\times \left( length+breadth \right)\times height$
The area of 4-walls (internal walls) of the box= $2\times \left( 1.42+1.10 \right)\times 0.80$
$\begin{align}
  & =\left[ 2\times \left( 2.52 \right)\times 0.80 \right]{{m}^{2}} \\
 & =4.032{{m}^{2}} \\
\end{align}$
Area of the internal base of the box = internal length $\times $ internal breadth
$\begin{align}
  & =1.42\times 1.10{{m}^{2}} \\
 & =1.562{{m}^{2}} \\
\end{align}$
Total internal surface area of the box will be the sum of the area of 4-walls and area of the base of the box. We are not taking top surface area because it is an open box.
So,
Total internal surface area
$\begin{align}
  & =4.032{{m}^{2}}+1.562{{m}^{2}} \\
 & =\left( 4.032+1.562 \right){{m}^{2}} \\
 & =5.594{{m}^{2}} \\
\end{align}$
According to question, cost of painting is Rs 50 per square meter, i.e. Rs. 50 for painting 1 sq. meter.
We have to paint an area of $5.594{{m}^{2}}$.
Using unitary method-
1 sq. meter costs Rs 50
So, 5.594 sq. meter will cost
$\begin{align}
  & =Rs\,\left( 50\times 5.594 \right) \\
 & =Rs\,279.70 \\
\end{align}$
Hence the total cost of painting the internal surface of the box will be Rs 279.70.
So, option (a) is the answer.

Note: In the question, dimensions are given as different units. But to use in formula, convert the dimensions into the same unit first then calculate further. Also, remember that it is an open box. So, do not write internal height = external height – (2 $\times $ thickness) . It is wrong. Such mistakes will lead to wrong answers and hence should be avoided.