Question

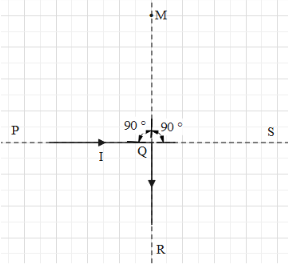
An infinitely long conductor PQR is bent to form a right angle as shown in figure. A current I flows through PQR. The magnetic field due to this current carrying conductor at the point M is ${{B}_{1}}$. Now, another infinitely long straight conductor QS, is connected at Q so that the current is $\dfrac{I}{2}$ in QR as well as in QS, the current in PQ remaining unchanged. The magnetic field at M is now ${{B}_{2}}$. The ratio $\dfrac{{{B}_{1}}}{{{B}_{2}}}$ is given by

 A. $\dfrac{1}{2}$
B. $1$
C. $\dfrac{2}{3}$
D. $2$

Answer 1

Hint:Use the formula for the magnitude of the magnetic field at a point P due to a straight current carrying conductor and the right hand thumb rule to find the direction of the magnetic field. With these find the magnetic field in both the case and then calculate the ratio of both.

Formula used:
$B=\dfrac{{{\mu }_{0}}I}{4\pi d}\left( sin{{\theta }_{1}}+sin{{\theta }_{2}} \right)$
where ${{\mu }_{0}}$ is the permeability of free space, I is the current in the conductor and ${{\theta }_{1}}$, ${{\theta }_{2}}$ are the angles .

Complete step by step answer:
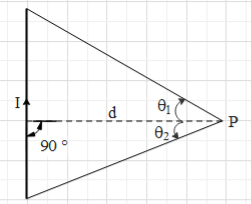
Consider a straight current carrying conduction of length l. The magnitude of the magnetic field at a point P, which is at a perpendicular d from the conductor as shown in the figure is given as $B=\dfrac{{{\mu }_{0}}I}{4\pi d}\left( sin{{\theta }_{1}}+sin{{\theta }_{2}} \right)$,
where ${{\mu }_{0}}$ is the permeability of free space, I is the current in the conductor and ${{\theta }_{1}}$, ${{\theta }_{2}}$ are the angles as shown in the figure.

The direction of the magnetic field is given by the right hand thumb rule.In the first case, the magnetic field at point M due the current in QR is zero since it passes through the axis of QR. The magnetic field at the same point due to current in PQ is ${{B}_{1}}=\dfrac{{{\mu }_{0}}I}{4\pi d}\left( sin(0)+sin{{90}^{\circ }} \right)$.
(since the conductor is infinitely long, ${{\theta }_{2}}\approx {{90}^{\circ }}$).
And $\sin {{90}^{\circ }}=1$, $\sin {{0}^{\circ }}=0$.
${{B}_{1}}=\dfrac{{{\mu }_{0}}I}{4\pi d}$ …. (i).
From the right hand thumb rule, the direction of ${{B}_{1}}$ is outwards the plane.

In the second case too, the magnetic field at point M due to QR is zero. The magnetic field at the same point due to the current in PQ is ${{B}_{PQ}}=\dfrac{{{\mu }_{0}}I}{4\pi d}$.The magnetic field due to the current in QS is,
${{B}_{QS}}=\dfrac{{{\mu }_{0}}\left( \dfrac{I}{2} \right)}{4\pi d}\left( sin{{90}^{\circ }}+sin(0) \right)\\
\Rightarrow{{B}_{QS}} =\dfrac{{{\mu }_{0}}\left( \dfrac{I}{2} \right)}{4\pi d}\\
\Rightarrow{{B}_{QS}} =\dfrac{{{\mu }_{0}}I}{8\pi d}$.
From the right hand thumb rule, the direction of both ${{B}_{PQ}}$ and ${{B}_{QS}}$ are parallel and outwards the plane.This means that the net magnetic field due to the set up is ${{B}_{2}}={{B}_{PQ}}+{{B}_{QS}}$.
$\Rightarrow {{B}_{2}}=\dfrac{{{\mu }_{0}}I}{4\pi d}+\dfrac{{{\mu }_{0}}I}{8\pi d}$.
$\Rightarrow {{B}_{2}}=\dfrac{3{{\mu }_{0}}I}{8\pi d}$ …. (ii).
Now divide (i) by (ii).
$\Rightarrow \dfrac{{{B}_{1}}}{{{B}_{2}}}=\dfrac{\dfrac{{{\mu }_{0}}I}{4\pi d}}{\dfrac{3{{\mu }_{0}}I}{8\pi d}}\\
\therefore \dfrac{{{B}_{1}}}{{{B}_{2}}} =\dfrac{2}{3}$.
With this we found the value of the ratio.

Hence, the correct option is C.

Note: In the formula for the magnitude of magnetic field that we discussed above, we see that the magnetic field due to PQ and QS is directly proportional to current because all the other factors are the same for both. Therefore, this means that in the second case ${{B}_{QS}}=\dfrac{{{B}_{PQ}}}{2}$, since the current in QS is half of the current in PQ.
$\Rightarrow {{B}_{2}}={{B}_{PQ}}+\dfrac{{{B}_{PQ}}}{2}\\
\Rightarrow {{B}_{2}} =\dfrac{3{{B}_{PQ}}}{2}$.
And in the first case ${{B}_{1}}={{B}_{PQ}}$.
When we divide both, we get that $\dfrac{{{B}_{1}}}{{{B}_{2}}}=\dfrac{{{B}_{PQ}}}{\dfrac{3{{B}_{PQ}}}{2}}$
$\Rightarrow \dfrac{{{B}_{1}}}{{{B}_{2}}}=\dfrac{2}{3}$.