Question

An electric field prevailing in a region depends only on ${\text{X}}$ and ${\text{Y}}$ coordinates according to an equation, $\mathop {\text{E}}\limits^ \to = {\text{b}}\dfrac{{{\text{X}}\mathop {\text{i}}\limits^ \wedge {\text{ + Y}}\mathop {\text{j}}\limits^ \wedge }}{{{{\text{X}}^2}{\text{ + }}{{\text{Y}}^2}}}$ where $b$ is a constant. Find the flux passing through a sphere of radius $r$ whose center is on the origin of the coordinate system.

Answer 1

Hint: The rate of flow of the electric field through a given area is called electric flux. It is proportional to the number of electric field lines passing through a virtual surface. It is depicted as lines in a plane that intersects or contains electric charge poles or magnetic poles.


Complete step-by-step solution:
Consider a sphere with its center at the origin. The flux is given by $\Phi = \int {\mathop {\text{E}}\limits^ \to .} \mathop {{\text{ds}}}\limits^ \to = \dfrac{{{q_{in}}}}{{{\varepsilon _ \circ }}}$ . If the given sphere is enclosed in a uniform cylinder, then obviously the net charge will be the same and the flux passing through the given sphere is the same as the flux passing through the cylinder. The flux through cylinder is given by $\Phi = \int {\mathop {\text{E}}\limits^ \to .} \mathop {{\text{ds}}}\limits^ \to $ . The radius is $R$ and all the points which are at a distance $R$ from the center will have the same electric field as the cylinder is symmetrical. As the electric field is constant, the flux will be $\Phi = \mathop {\text{E}}\limits^ \to \int {\mathop {{\text{ds}}}\limits^ \to } $ . Here, $\int {\mathop {{\text{ds}}}\limits^ \to } $ means the lateral surface area.
Let us draw a sphere of radius $R$ inside a closed cylinder of length $L$ and center of sphere is at the origin O. the diagram is shown as

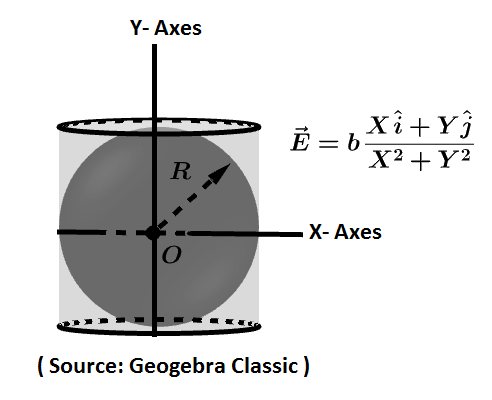
The lateral surface area of cylinder is: $2\pi RL$
Where $L = $ height of cylinder
From the figure, we can say that the height of cylinder is $2R$
$\Phi = \mathop {\text{E}}\limits^ \to .2\pi r(2R)$
$\Phi = \mathop {\text{E}}\limits^ \to .4\pi {R^2}$
The magnitude of $\mathop {\text{E}}\limits^ \to $ is given by
$\left| {\mathop {\text{E}}\limits^ \to } \right| = \left| {{\text{b}}\dfrac{{\left( {{\text{X}}\mathop {\text{i}}\limits^ \wedge {\text{ + Y}}\mathop {\text{j}}\limits^ \wedge } \right)}}{{{{\text{X}}^2}{\text{ + }}{{\text{Y}}^2}}}} \right|$
$ = \dfrac{{{\text{b}}\sqrt {{{\text{X}}^{\text{2}}}{\text{ + }}{{\text{Y}}^{\text{2}}}} }}{{{{\left( {\sqrt {{{\text{X}}^{\text{2}}}{\text{ + }}{{\text{Y}}^{\text{2}}}} } \right)}^2}}}$
$ = \dfrac{b}{{\sqrt {{{\text{X}}^{\text{2}}}{\text{ + }}{{\text{Y}}^{\text{2}}}} }}$
Now, consider an arbitrary point $(x,y)$ on the sphere. Using the distance formula we can calculate the distance between the point and origin. The distance is $\sqrt {{x^2} + {y^2}} $ . Also, the distance is equal to the radius of the sphere. So $R = \sqrt {{x^2} + {y^2}} $ . Use this in the magnitude of electric field expression.
$\left| {\mathop {\text{E}}\limits^ \to } \right| = \dfrac{b}{{\sqrt {{{\text{X}}^{\text{2}}}{\text{ + }}{{\text{Y}}^{\text{2}}}} }}$
$ = \dfrac{b}{R}$
Now, the electric flux is given as $\left| \Phi \right| = 4\pi b{R^2} \times \dfrac{1}{R}$
Hence, the magnitude of electric flux through the sphere is $\Phi = 4\pi bR$

Note: Electric field is defined as the electric force per unit charge. The electric flux through an area is the electric field multiplied by the area of the surface projected in a plane that is perpendicular to the field. The total number of electric field lines passing through a given area in a unit time is called the electric flux.