Question

AM is a median of a triangle ABC. Is $AB+BC+CA>2AM$?
(Consider the sides of triangles $\Delta ABM\ and\ \Delta AMC$)
A. True
B. False

Answer 1

Hint: We will first start by drawing a rough diagram of the situation. Then we will use the fact that the sum of two sides of a triangle is greater than or equal to the third side in the two triangles formed by the median and use it to find the answer.

Complete step-by-step answer:
Now, we have been given that AM is a median of a triangle ABC.

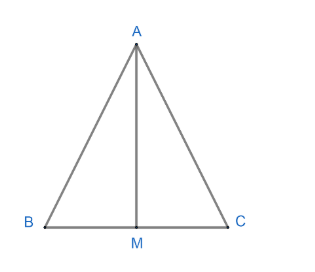
Now, we know that the sum of two sides of a triangle is always greater than or equal to the third side. So, we use this in $\Delta ABM\ and\ \Delta AMC$.
Now, in $\Delta ABM$ we have,
$AB+BM\ge AM..........\left( 1 \right)$
Now, in $\Delta AMC$ we have,
$AC+MC\ge AM..........\left( 2 \right)$
Now, adding () and (2) we have,
$AB+BM+MC+AC\ge 2AM$
Now, we know that $BM+MC=BC$. So, we have,
$AB+BC+AC>2AM$
Hence, the correct answer is (A) True.

Note: It is important to note that we haven’t used the fact that AM is the median of $\Delta ABC$ to find the answer. Therefore, the relation that $AB+BC+CA>2AM$ is true in general irrespective of the fact that whether AM is median or not.