Question

All x satisfy the inequality
\[{{\left( {{\cot }^{-1}}x \right)}^{2}}-7\left( {{\cot }^{-1}}x \right)+10>0\], lie in the interval
(a) \[\left( -\infty ,\cot 5 \right)\cup \left( \cot 4,\cot 2 \right)\]
(b) \[\left( \cot 5,\cot 4 \right)\]
(c) \[\left( \cot 2,\infty \right)\]
(d) \[\left( -\infty ,\cot 2 \right)\cup \left( \cot 5,\infty \right)\]

Answer 1

Hint: First of all, let \[{{\cot }^{-1}}x=y\] and resolve the equation into factors and find the range of \[y={{\cot }^{-1}}x\]. Then draw the graph of \[{{\cot }^{-1}}x\] to examine the values of x. Consider the domain and range of \[{{\cot }^{-1}}x\] properly for the correct values of x.

Complete step-by-step answer:
We are given that \[{{\left( {{\cot }^{-1}}x \right)}^{2}}-7\left( {{\cot }^{-1}}x \right)+10>0\].
Here, we have to find the values of x which satisfies this inequality.

Let us consider the inequality given in the question.
\[{{\left( {{\cot }^{-1}}x \right)}^{2}}-7\left( {{\cot }^{-1}}x \right)+10>0\]
Let us consider \[{{\cot }^{-1}}x\] to be y. By substituting \[{{\cot }^{-1}}x=y\] in the above inequality, we get,
\[{{y}^{2}}-7y+10>0\]

Here, we can write 7y = 5y + 2y. So, we get,
\[{{y}^{2}}-5y-2y+10>0\]
We can write the above inequality as,
\[y\left( y-5 \right)-2\left( y-5 \right)>0\]
By taking out (y – 5) common, we get,
\[\left( y-5 \right)\left( y-2 \right)>0\]

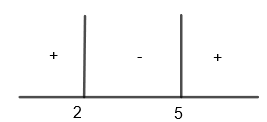
If y > 5, then (y – 5) > 0 and (y – 2) > 0.
So, we get (y – 5) (y – 2) > 0

Hence, y > 5 satisfies the inequality.
For example, let us take y = 7. By substituting y = 7, we get,
\[\left( 7-5 \right)\left( 7-2 \right)=\left( 2 \right)\left( 5 \right)=10>0\]
So, we get, \[y\in \left( 5,\infty \right)\].
If 2 < y < 5, then (y – 5) < 0 and (y – 2) > 0
So, we get (y – 5) (y – 2) < 0

Hence, 2 < y < 5 does not satisfy the inequality.

For example, let us take y = 3. By substituting y = 3, we get,
\[\left( 3-5 \right)\left( 3-2 \right)=\left( -2 \right)\left( 1 \right)=-2<0\]
So, we get, \[y\notin \left( 2,5 \right)\].
If y < 2, then (y – 5) < 0 and (y – 2) < 0.
So, we get, (y – 5) (y – 2) > 0

Hence y < 2 satisfies the inequality.
For example, let us take y = 0. By substituting y = 0, we get,
\[\left( 0-5 \right)\left( 0-2 \right)=\left( -5 \right)\left( -2 \right)=10>0\]
So, we get \[y\in \left( -\infty ,2 \right)\].
Hence, we get \[y\in \left( -\infty ,2 \right)\cup \left( 5,\infty \right)\].
We had assumed that \[{{\cot }^{-1}}x=y\], so by substituting \[y={{\cot }^{-1}}x\], we get,
\[{{\cot }^{-1}}x\in \left( -\infty ,2 \right)\cup \left( 5,\infty \right)\]
So, we get \[{{\cot }^{-1}}x<2\] and \[{{\cot }^{-1}}x>5\].

Now, we will see the graph of \[{{\cot }^{-1}}x\], that is

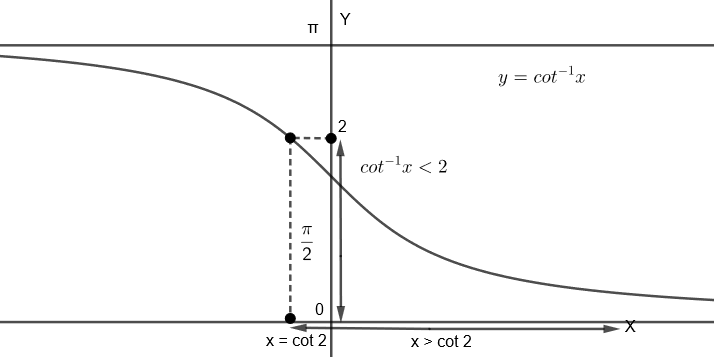
We know that the range of \[{{\cot }^{-1}}x\] is \[\left( 0,\pi \right)\], so it can’t be greater than 5.

Now, considering \[{{\cot }^{-1}}x<2\]
From the graph, we can see that, for \[{{\cot }^{-1}}x<2,\text{ }x>\cot 2\]
So, we get \[x\in \left( \cot 2,\infty \right)\].

Hence, the correct answer is option (c).

Note: After getting \[{{\cot }^{-1}}x\in \left( -\infty ,2 \right)\cup \left( 5,\infty \right)\], students often make this mistake of calculating x as \[x\in \left( -\infty ,\cot 2 \right)\cup \left( \cot 5,\infty \right)\] but this is wrong as we know that \[{{\cot }^{-1}}x\] could not be greater than 5 because its range is \[\left( 0,\pi \right)\]. Also for \[{{\cot }^{-1}}x\in \left( -\infty ,2 \right)\], \[x\in \left( \cot 2,\infty \right)\] not \[\left( -\infty ,\cot 2 \right)\]. So for inverse trigonometric function, it is advisable to first draw the graph and then only examine the values of x for the correct results.