Question

ABCDE is a pentagon. If the sum of the vectors AB + AE + BC + DC + ED + AC = \[\lambda \]AC , then find the value of $\lambda $.

Answer 1

Hint: Here in this problem applying the triangle law of vector addition which is says that addition of any the vectors in one particular order gives a null vector, i.e, in a triangle the sides of the vectors add to give a zero vector whereas the addition of the two vectors gives the resultant vector. Therefore, the set of vectors of addition in a closed polygon, the resultant of these vectors will be a null vector.

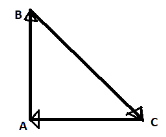
Here $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = 0$, addition of the vectors in one order of a closed polygon gives a null vector
$\because \overrightarrow {CA} = - \overrightarrow {AC} $
$\overrightarrow {AB} + \overrightarrow {BC} - \overrightarrow {AC} = 0$
$\therefore \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} $

Complete step-by-step solution:
$ \Rightarrow \overrightarrow {AB} + \overrightarrow {AE} + \overrightarrow {BC} + \overrightarrow {DC} + \overrightarrow {ED} + \overrightarrow {AC} $
Here consider the sides $AB,BC$ and $CA$ forms a triangle,
Therefore the addition of the vectors $\overrightarrow {AB} + \overrightarrow {BC} $ gives,
From the figure it is visible that the resultant of
$\therefore \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} $
Now consider the vector terms $\overrightarrow {AE} + \overrightarrow {ED} + \overrightarrow {DC} $,
As it forms a quadrilateral with sides $AE,ED,DC$ and $CA$.
$\therefore \overrightarrow {AE} + \overrightarrow {ED} + \overrightarrow {DC} + \overrightarrow {CA} = 0$
$ \Rightarrow \overrightarrow {AE} + \overrightarrow {ED} + \overrightarrow {DC} = \overrightarrow {AC} $
Now consider L.H.S = $\overrightarrow {AB} + \overrightarrow {AE} + \overrightarrow {BC} + \overrightarrow {DC} + \overrightarrow {ED} + \overrightarrow {AC} $
Grouping the terms together,
\[ \Rightarrow \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {AE} + \overrightarrow {ED} + \overrightarrow {DC} + \overrightarrow {AC} \]
$ \Rightarrow \overrightarrow {AC} + \overrightarrow {AC} + \overrightarrow {AC} $
$ \Rightarrow 3\overrightarrow {AC} $
Now consider R.H.S = $\lambda \overrightarrow {AC} $
$3\overrightarrow {AC} = \lambda \overrightarrow {AC} $
$\therefore \lambda = 3$

The value of the $\lambda = 3$

Note: Remember when naming the vector AB = $\overrightarrow {AB} $, this means that the head of the vector is at A and the tail of the vector is at B. $\overrightarrow {AB} = B - A$.
Also another point to be noted is that the direction of the vector changes when the sign changes, i.e, when $ - \overrightarrow {AB} = \overrightarrow {BA} $ , here the tail of the vector is B and head becomes A.