Question

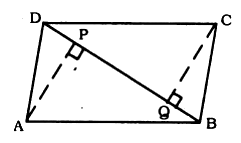
ABCD is a parallelogram and AP and CQ are perpendicular from vertices A and C on diagonal BD. Show that ΔAPB ≅ ΔCQD.

Answer 1

Hint: Two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other. The various congruence conditions that may be used to show congruence of triangles are -
1) SSS - Side Side Side
2) SAS - Side Angle Side
3) ASA - Angle Side Angle
4) AAS - Angle Angle Side
5) RHS - Right Hypotenuse Side
Use ASA congruence rules for the given triangles to show congruence.

Complete step-by-step answer:
Given: ABCD is a parallelogram. AP and CQ are perpendicular to BD
To Prove: ΔAPB ≅ ΔCQD
As AB is parallel to CD (property of parallelogram),
∠ABP = ∠CDQ (Alternate interior angles)
AB = CD (Opposite sides of a parallelogram are equal)
∠APB = ∠CQD = 90° (Right Angles)
Therefore,
ΔAPB ≅ ΔCQD (By ASA Congruence Rule)
As ΔAPB ≅ ΔCQD, so, we can say that the corresponding sides of the triangle are also equal, i.e.
AP = CQ (By CPCT)
Hence proved.

Note: One must know about the CPCT rule.
CPCT stands for ‘corresponding parts of congruent triangles’. CPCT theorem states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other.
There are four different types of Congruence Rules:-
1) SSS CONGRUENCE OF TWO TRIANGLES: Two triangles are congruent if the three sides of one of them are equal to the three corresponding sides of the other. This is called SSS congruence of Triangles.
2) SAS CONGRUENCE OF TWO TRIANGLES: Two triangles are congruent if two sides and the angle included between them in one of the triangles are equal to the corresponding sides and the angle included between them of the other triangle. This is called SAS congruence of Triangles.
3) ASA CONGRUENCE OF TWO TRIANGLES: Two triangles are congruent if two angles and the side included between them in one of the triangles are equal to the corresponding angles and the side included between them of the other triangle. This is called ASA congruence of Triangles.
4) RHS CONGRUENCE OF TWO RIGHT- ANGLED TRIANGLES: Two right - angled triangles are congruent if the hypotenuse and a leg of one of the triangles are equal to the hypotenuse and the corresponding leg of the other triangle. This is called RHS congruence of right- angled triangles.