Question

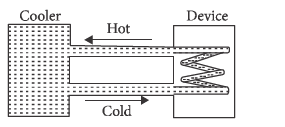
A water cooler of storage capacity $ 120litres $ can cool water at a constant rate of $ P $ with in a closed circulation system (as shown schematically in the figure), the water from the cooler is used to cool an external device that generates constantly $ 3kW $ of heat (thermal load). The temperature of water fed into the device cannot exceed $ 30^\circ C $ and the entire stored $ 120litres $ of water is initially cooled to $ 10^\circ C $ . The entire system is thermally insulated. The minimum value of $ P $ (in watts) for which the device can be operated for $ 3hours $ is:
(Specific heat of water is $ 4.2\;kJk{g^{ - 1}}{K^{ - 1}}\; $ and density of water is $ 1000\;kg\;{m^{ - 3}} $ )

(A) $ \;1600 $
(B) $ 2067 $
(C) $ 2533 $
(D) $ 3933 $

Answer 1

Hint : We can see that the units of the given values in the question are of different systems, we first convert all the units to the SI system before we start to solve this question. After converting the units, we find the net energy generated. This is equal to the amount of heat generated or the heat absorbed by water. From the net energy equation, we find the value of $ P $

Formula used: Energy is equal to $ E = pt $
Here, power is represented by $ p $, Time is represented by $ t $
Heat energy is equal to $ h = m{c_p}\Delta T $
Here, mass is represented by $ m $, Specific heat capacity is represented by $ {c_p} $ , Change in temperature is represented by $ \Delta T $ .

Complete step by step answer
From the question the power generated by the device is
 $ {p_g} = 3kW = 3 \times {10^3}W $
Let us take power absorbed as $ p $
Time $ t = 3hours = 3 \times 60 \times 60sec $
From energy formula, the net energy generated is $ ({p_g} - p)t = (3 \times {10^3} - p) \times (3 \times 3600) $
Heat absorbed by water is $ h = m{c_p}\Delta T $
Heat absorbed is represented by $ h $
Mass is represented by $ m $
Since the mass of water is not given, we calculate it from the density of water
Mass is equal to density times volume
 $ m = \rho \times v = 120 \times 1 $
Substituting in heat absorbed formula
 $ h = m{c_p}\Delta T $
 $ \Rightarrow h = 120 \times 4.2 \times {10^3} \times (30 - 10) $
Here the final and initial temperatures are $ 30 $ , $ 10 $
Specific heat is represented by $ {c_p} = 4.2 \times {10^3}Jk{g^{ - 1}}{K^{ - 1}} $
The heat energy generated and absorbed are equal
 $ ({p_g} - p)t = m{c_p}\Delta T $
 $ \Rightarrow pt = {p_g}t - m{c_p}\Delta T $
 $ \Rightarrow pt = ((3 \times {10^3})(3 \times 3600)) - (120 \times 4.2 \times {10^3} \times (30 - 10)) $
 $ \Rightarrow pt = 223.2 \times {10^5}WH $
 $ \therefore p = \dfrac{{223.2 \times {{10}^5}}}{{3600}}W = 2067W $
Hence the minimum value of $ p $ for which the device can be operated for three hours is $ 2067W $
Option (B); $ 2067W $ is the correct answer.

Note
Students might make a mistake by not converting the units to SI units. Since the final answer is to be found in SI units all the given values should be converted to SI units and then proceed to solve the question. Also, while finding the mass of water we need to convert the units of volume of water from liters to cubic meter.