Question

A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are 6cm and 4cm respectively. Find the height of water in a cylinder.

Answer 1

Hint: According to the question given above we have to find the height of the water in the cylinder so, first of all we let the height of the water in the cylinder. As given in the question water was in the vessel form of hemispherical bowl and it (water) was emptied in the vessel form of cylinder. So, we can say that volume of water in the hemispherical bowl is equal to the volume of water in the cylinder we can also understand it with the help of diagram given below:

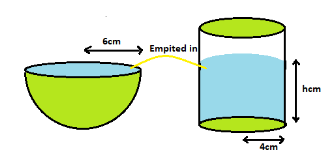
As we can see in the diagram water mentioned in sky blue colour is filled up to the height $hcm.$ Which was kept in the vessel, hemispherical in shape.

Formula used: Volume of hemisphere $ = \dfrac{2}{3}\pi {r^3}$……………………………….(1)

Where, r is the radius of the hemispherical bowl
Volume of cylinder$ = \pi {r^2}h$ ……………………………………..(2)
Where, r is the radius of the cylinder and h is the height of the cylinder.

On comparing both of the volumes we can find the height to which the water is filled in the vessel, cylinder in shape.

Complete step-by-step answer:
Given,
The internal radius of the hemispherical bowl = 6cm and,
The internal radius of the cylinder = 4cm.
Let, the height to which the water is filled in the cylinder = $hcm.$
Step 1: first of all we will find the volume of the hemispherical bowl, using the formula (1) to find the volume of the water it contains.
Hence,
Volume of the hemispherical bowl = volume of water in it,
$ = \dfrac{2}{3}\pi {(6)^3}$
As we know, the value of$\pi = \dfrac{{22}}{7}$.On substituting the value of $\pi $in the above equation.
$
   = \dfrac{2}{3} \times \dfrac{{22}}{7} \times 216 \\
   = \dfrac{{44 \times 72}}{7} \\
   = 452.5c{m^3} \\
$
Step 2: Now we will find the volume of the cylinder because the water contained in the hemispherical bowl was emptied into it.
Hence, to find the volume of the cylinder we will use the formula (2).On substituting all the values in the formula (2).
$ = \pi {(4)^2} \times h$
As we know, the value of $\pi = \dfrac{{22}}{7}$.On substituting the value of $\pi $ in the above equation.
$
   = \dfrac{{22}}{7} \times 16 \times h \\
   = \dfrac{{352}}{7}hc{m^3} \\
$
Step 3: As given in the question the water in the hemispherical bowl is emptied in the cylinder. So, we can say that the volume of water in the hemispherical bowl is equal to the volume of water in the cylinder, which is filled in the cylinder up to the height h(cm).
Hence,
Volume of water in the cylinder up to height h(cm) = Volume of hemispherical bowl
$\dfrac{{352}}{7} \times h = 452.5$
Step 4: On solving the equation obtained in step 3, we can find the height of water contained in the cylinder.
$
  h = \dfrac{{452.5 \times 7}}{{352}} \\
  h = \dfrac{{3167.5}}{{352}} \\
  h = 8.99 \approx 9cm \\
$
So, height of water in a cylinder = $9cm.$
Final solution: Hence, by finding the volumes of both of the vessels of different shapes (hemisphere and cylinder) and on comparing them, we have obtained the height of water $h = 9cm$ to which it was filled in the cylinder.

Note: As we know water is nearly incompressible fluid that conforms to the shape of its container but retains a constant volume. So, we can say that the volume of water in the hemisphere bowl is equal to the volume of water in the cylinder.
To make the calculations easy, we should not place the value of $\pi \left( {\dfrac{{22}}{7}or3.14} \right)$
Volume of water in cylinder = Volume of water in hemispherical bowl
$\pi {(4)^2}h = \dfrac{2}{3}\pi {(6)^3}$
On eliminating the $\pi $from both sides of the equation,
$
  16 \times h = \dfrac{{2 \times 216}}{3} \\
  h = \dfrac{{2 \times 72}}{{16}} \\
  h = 9cm. \\
$
Hence, the height of water in the cylinder $h = 9cm.$