Question

What is a vertical asymptote in calculus?

Answer 1

Hint: To solve this question you should know about the asymptotes or vertical asymptotes. Any vertical asymptote is a place where the function is undefined and the limit of that function does not exist. This is happening because as 1 approaches to the asymptote, even any small shift in the x – value leads to arbitrarily large fluctuations in the value of the functions.

Complete step by step answer:
According to our question we have to explain about the vertical asymptote in calculus.
So, in calculus a vertical asymptote is a place where the function is undefined and the limits of that function does not exist.
In simple words we can say that –
“Definition : The line \[x=a\] is called a vertical asymptote of the curve \[y=f\left( x \right)\] if at least one of the following statement is true: -
\[\begin{align}
  & \underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)=-\infty \\
 & \underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)=\infty \\
 & \underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)=-\infty \\
 & \underset{x\to {{a}^{+}}}{\mathop{\lim }}\,f\left( x \right)=\infty \\
 & \underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=-\infty \\
 & \underset{x\to a}{\mathop{\lim }}\,f\left( x \right)=\infty '' \\
\end{align}\]
In this definition the superscript + denotes the right hand limits of \[f\left( x \right)\] as \[x\to a\], and the superscript – denotes the left hand limits of \[f\left( x \right)\] as \[x\to a\].
If we take an example and consider the function \[f\left( x \right)=\dfrac{1}{x}\], if we approach \[x=0\] from the left or right, \[f\left( x \right)\] becomes arbitrarily negative or arbitrarily positive respectively.
In this condition two of our statements are true from the definition. Especially the fourth and first. Therefore, we can say that:
\[f\left( x \right)=\dfrac{1}{x}\] has a vertical asymptote at \[x=0\]

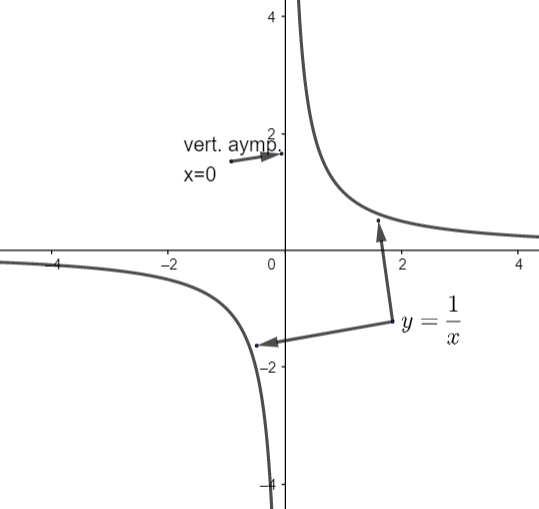
Note: For any vertical asymptote point it is compulsory that it is satisfying at least any one point which is defined in the definition. If that is not satisfying any point then it can’t be possible to be a vertical asymptote at that point in that function’s curve. And this is mandatory for every function.