Question

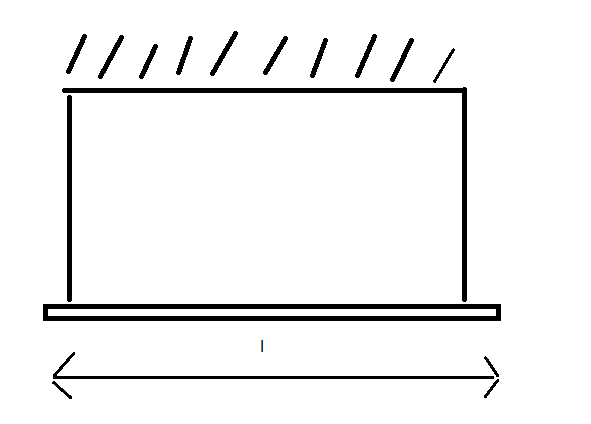
A uniform rod of mass m and length l is suspended by two strings at its ends as shown. When one of the strings is cut, the rod starts falling with an initial angular acceleration.

a) $\dfrac{{3g}}{l}$
b) $\dfrac{g}{{2l}}$
c) $\dfrac{{3g}}{{2l}}$
d) $\dfrac{{3g}}{{4l}}$

Answer 1

Hint: Torque is the rotational equivalent of linear force. It is also referred to as the moment, moment of force, rotational force or turning effect, depending on the field of study. Just a linear force is a push or a pull, a torque can be thought of as a twist of an object about a specific axis.

Complete step by step solution:
When the string is cut, the torque acting on the rod due to gravity is
$\tau = rF\sin \theta $where $\tau $ is the torque due to gravity , F is the force acting on the rod while r is the length of the rod and $\theta $ is the angle at which the torque acts on the rod .
Since F= mg and r=l, we have
$\tau = mgl\sin \theta $
Now , $\theta $= $90^\circ $

Therefore, we have,
$\tau = mgl$
Moment of inertia of rod about an axis passing through one end is
$I = \dfrac{{m{l^2}}}{3}$
We know that
${\text{Torque = Moment of Inertia }} \times {\text{ Acceleration }}$
$ \Rightarrow \tau = I \times a$
On taking a as the subject of the formula,
$ \Rightarrow a = \dfrac{\tau }{I}$
Now equating the formulas that we have gotten earlier,
$ \Rightarrow a = \dfrac{{mgl}}{{m{l^2}}} \times 3$
On simplifying we get,
$ \Rightarrow a = \dfrac{{3g}}{l}$

Thus, the required option is a) $\dfrac{{3g}}{l}$

Note: Before being able to solve the sum, students need to be able to understand the concept of torque. Also, they need to be able to derive all the formulas for the same.