Question

A uniform half meter ruler balances horizontally on a knife-edge at 29cm mark when a weight of 20g is suspended from one end. What is the weight of the half meter ruler?

Answer 1

Hint: You could read the question well as a very first step, thus you could note down the given points. You could then recall the condition to be followed for the scale to be balanced at the knife edge. Then you could do the substitutions accordingly and hence find the answer.

Complete step-by-step solution:
In the question, we are given a uniform half meter ruler that is balanced horizontally on a knife edge at 29cm mark on a 20g weight being suspended on one end. We are supposed to find the weight of the half meter ruler using this information.
The given conditions could be depicted in a diagram as:

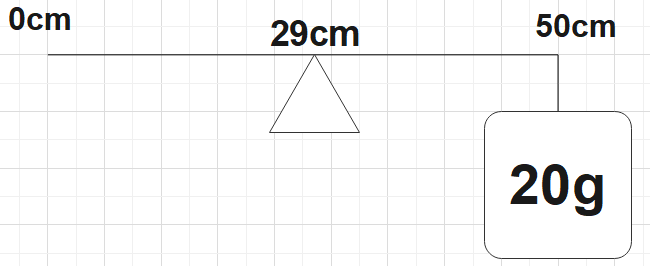
The centre of gravity of the given scale will at 25cm (midpoint of a half meter scale). The distance of the balance point and the centre of gravity (Y),
Y= 29-25=4cm.
Now the distance of the end at which the weight is hung form the pivot point (X),
X=50-29=21cm
Weight of the meter rule = $\dfrac{X}{Y}\times $suspended weight
$W=\dfrac{21}{4}\times 20$
$\therefore W=105g$
Therefore, we found the weight of the given half meter scale to be 105g.

Note: In the solution, what we have actually done is that we have balanced the moments of inertia about the pivoted point. At equilibrium we have assumed the moment in the anti-clockwise direction to be equal to that in the clockwise direction and hence carried out the calculation accordingly.
${{v}_{\min }}=\sqrt{rg}$