Question

A uniform electric field of \[100V{{m}^{-1}}\] is directed at ${{30}^{\circ }}$ with the positive x - axis as shown in fig. Find the potential difference, $VBA$ if OA=2m and OB=4m.
 

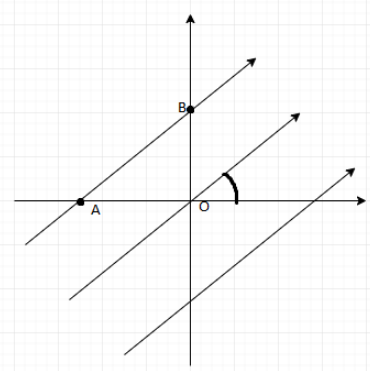
Answer 1

Hint: We can find more information from the given figure by forming an equipotential surface that is perpendicular to the given electric field.

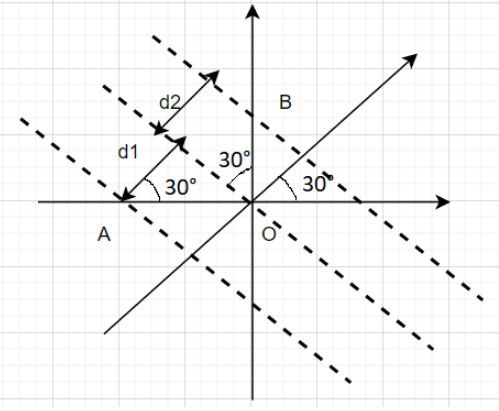
This forms two small right triangles within the figure. When we use its sides and angles, we can continue the calculation to find the potential difference.

Formulas used:
$V=E\times d$
where $V$ is the potential at a point, $E$ is the electric field and $d$ is the distance of separation.

Complete step by step answer:
From the modified figure,
\[{V_B}-{V_A}=100(\sqrt{3}+2)V\]
\[{d_1}=AO cos{{30}^{\circ }}\\
\Rightarrow {d_1} =\dfrac{2\sqrt{3}}{2}
\Rightarrow {d_1} =\sqrt{3}m\]
\[\Rightarrow {d_2}=BOsin{{30}^{\circ }}\\
\Rightarrow {d_2} =4\times \dfrac{1}{2}\\
\Rightarrow {d_2} =2m\]
\[{V_A}-{V_0}=E {d_1}\\
\therefore{V_A}-{V_0}=100\sqrt{3}V\]
We’re given that A lies on the X axis. However it can be moved forward along the equipotential surface lines and can be aligned with B to make our calculations easier. Hence, potential difference between initial point A and final point B in the same electric field E is given by
\[{V_A}-{V_B}=E({d_1}+{d_2})=100(\sqrt{3}+2)V\] or \[{V_B} - {V_A} =100(\sqrt{3}+2)V\]

Note:Equipotential surfaces are always created perpendicular to the field and they never intersect. For a point charge, these are concentric circles and for a uniform electric field, the equipotential surfaces are planes normal to the x-axis. The potential is constant inside a hollow charged spherical conductor . This can be treated as equipotential volume. No external work is required to move a charge from the centre to the surface. For an isolated point charge, the equipotential surface is a sphere. i.e. concentric spheres around the point charge are different equipotential surfaces.