Question

A typist uses a sheet measuring 20 cm by 30 cm length wise. If a margin of 2 cm is left on each side and a 3 cm margin on top and bottom, then the percent of page used for typing is:

(a) 40
(b) 60
(c) 64
(d) 72

Answer 1

Hint: We start solving the problem by find the area of the total page using the fact that the area of the rectangle with length l units and b units is $lb uni{{t}^{2}}$. We then find the dimensions of the part of the paper at which it is used for typing. We then find the area of the part of paper that is used for typing. We then find the percent of paper to type using $\%typing=\dfrac{Area\ of\ paper\ used\ for\ typing}{Total\ area\ of\ paper}\times 100$.

Complete step-by-step answer:
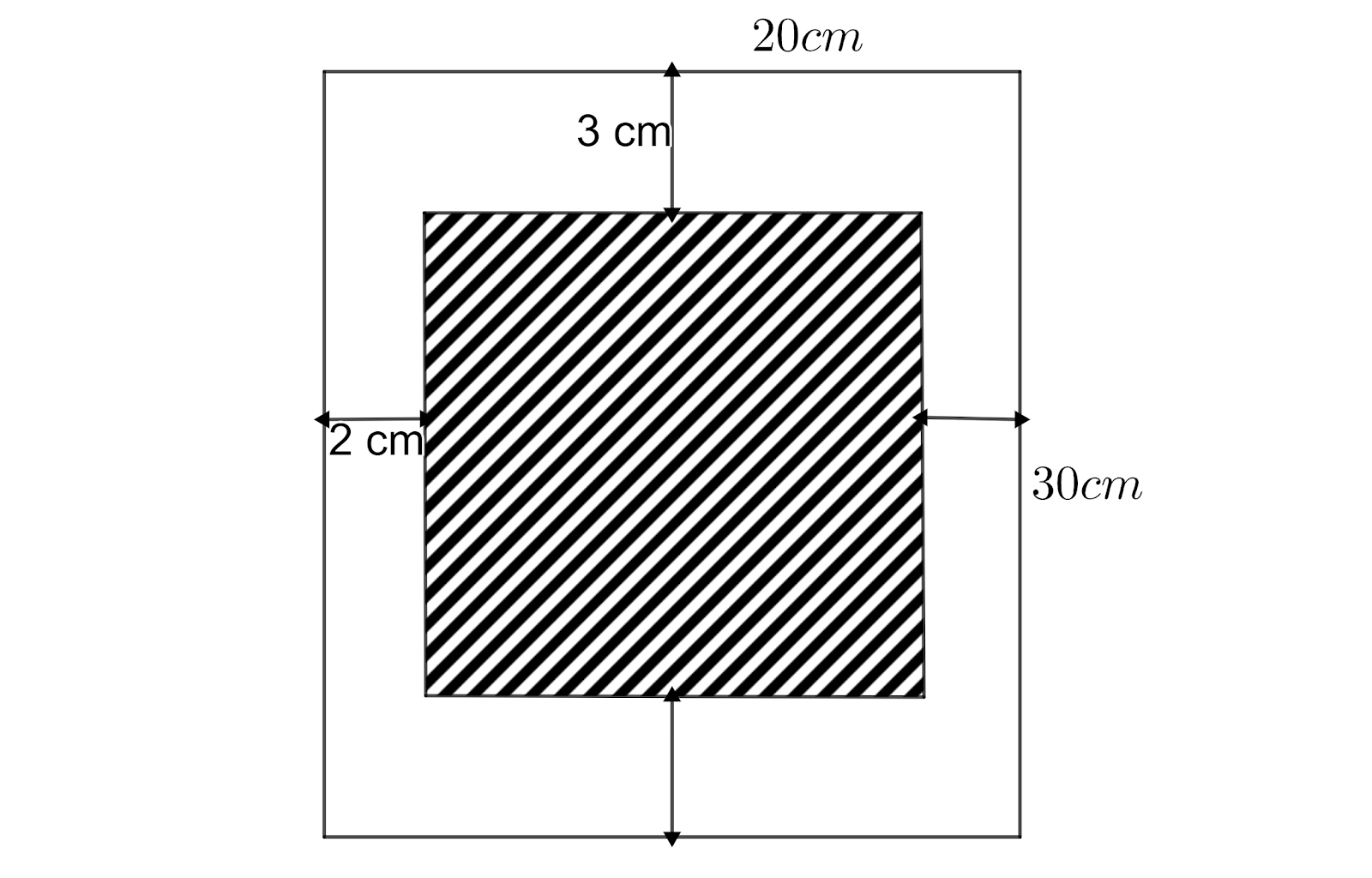
According to the problem, the typist uses the page measuring 20 cm and 30 cm lengthwise. If a margin of 2 cm is left on each side and a 3 cm margin on top and bottom, we need to find the total percent used for typing.
Let us find the total area of the paper used by the typist. From the figure, we can see that the paper resembles a rectangle with length 30 cm and breadth 20 cm.
We know that the area of the rectangle with length l units and b units is $lb uni{{t}^{2}}$.
So, the area of the total paper $A=20\times 30=600c{{m}^{2}}$.
Now, let us find the length of the part which is used for typing. We can see that the 3 cm is left at both top and bottom.
So, the length of the typing part is $\left( 30-\left( 3+3 \right) \right)=\left( 30-6 \right)=24 cm$.
Now, let us find the breadth of the part which is used for typing. We can see that the 2 cm is left on both sides.
So, the breadth of the typing part is $\left( 20-\left( 2+2 \right) \right)=\left( 20-4 \right)=16 cm$.
Now, let us find the area of the typing part. We can see that the typing part resembles a rectangle with 24 cm and breadth 16 cm.
So, the area of the typing part is $24\times 16=384c{{m}^{2}}$.
Now, we find the percentage of the total paper used for typing.
We have got $\%\ typing=\dfrac{Area\ of\ paper\ used\ for\ typing}{Total\ area\ of\ paper}\times 100$.
$\Rightarrow \%\ typing=\dfrac{384}{600}\times 100$.
$\Rightarrow \%\ typing=\dfrac{384}{6}$.
$\Rightarrow \%\ typing=64\%$.
So, we have found the percent of age used for typing as $64\%$.
∴ The correct option for the given problem is (c).

So, the correct answer is “Option (c)”.

Note: Here we have taken area to calculate the percentage as we can use total area of the paper to type. We use the perimeter if the paper is subjected to the conditions like bordering with colours, drawing the margins only at the edges. We should not just subtract only top or bottom to find the length of the typing area. Similarly, we should subtract both the left and right side of the page to get the required breadth.