Question

A thin lens of focal length $f$ and aperture diameter $d$ forms an image of intensity $I$ . If the central part of the aperture up to diameter $\dfrac{d}{2}$ is covered by an opaque paper, then find the new focal length and intensity of the image:
A) $\dfrac{f}{2}{\text{, }}\dfrac{I}{2}$
B) $\dfrac{f}{2}{\text{, }}\dfrac{3}{4}I$
C) $f{\text{, }}\dfrac{I}{2}$
D) $f{\text{, }}\dfrac{3}{4}I$

Answer 1

Hint: Covering up any portion of a lens by an opaque paper does not affect its focal length. However, the intensity of the image formed will decrease.

Complete step by step answer.
Step 1: Sketch a rough diagram to represent the problem at hand.
$\dfrac{d}{2}$

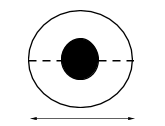
                     $d$
Step 2: List the data given in the question.
We have the focal length of the lens as $f$, its aperture diameter is $d$ and the intensity of the image formed is $I$.
Step 3: Find the area of the aperture when the central part of the aperture up to diameter $\dfrac{d}{2}$ is covered by an opaque paper.
Let ${A_1}$ denote the initial area of the aperture and ${A_2}$ denote the area once the aperture is covered by opaque paper.
Since the aperture is spherical, we have ${A_1} = \pi {\left( {\dfrac{d}{2}} \right)^2} = \dfrac{{\pi {d^2}}}{4}$ , where $\dfrac{d}{2}$ is the radius of the aperture.
The central part of the aperture up to diameter $\dfrac{d}{2}$ is now covered by an opaque paper.
Then the area will be, ${A_2} = \dfrac{{\pi {d^2}}}{4} - \dfrac{{\pi {{\left( {\dfrac{d}{2}} \right)}^2}}}{4}$
On simplifying we get, ${A_2} = \dfrac{{\pi {d^2}}}{4} - \dfrac{{\pi {d^2}}}{{16}}$ or, ${A_2} = \dfrac{{\pi {d^2}}}{4}\left( {1 - \dfrac{1}{4}} \right)$
Finally, we have ${A_2} = \dfrac{3}{4}\left( {\dfrac{{\pi {d^2}}}{4}} \right)$ .
Step 4: As intensity is proportional to the area, find the new intensity.
We have ${A_1} = \dfrac{{\pi {d^2}}}{4}$ and ${A_2} = \dfrac{3}{4}\left( {\dfrac{{\pi {d^2}}}{4}} \right)$ .
Express ${A_2}$ in terms of ${A_1}$ .
Now we have, ${A_2} = \dfrac{3}{4}{A_1}$ .
The intensity of the image is directly proportional to the area of the aperture of the lens.
Let ${I_1}$ be the initial intensity and ${I_2}$ be the intensity when the central part of the aperture was covered by an opaque paper.
i.e., $\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{{A_1}}}{{{A_2}}}$
Substituting ${A_1}$ and ${A_2}$ in the above relation and cancelling out the similar terms, we have $\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{4}{3}$ or, ${I_2} = \dfrac{3}{4}{I_1} = \dfrac{3}{4}I$ .
Therefore, the new intensity is $\dfrac{3}{4}I$. The intensity decreased as some light rays were blocked by the opaque paper.
Step 5: Discuss what happened to the focal length.
The focal remains the same when the central part of the aperture up to diameter $\dfrac{d}{2}$ was blocked by an opaque paper because the entire image will be formed by the light rays that were not blocked by the opaque paper.
Therefore, the focal length is $f$ .
The correct option is D) $f{\text{, }}\dfrac{3}{4}I$ .

Note: Focal length of the lens tells you how close one needs to be to the object that is to be captured. Far away objects demand a longer focal length while objects in front of you demand a smaller focal length.