Question

A thin film with an index of refraction of 1.50 coats a glass lens. The index of refraction of the glass is 1.60. What is the thinnest coating of film that will provide for very strongly reflected 546nm light (constructive thin film interference)?
A. 171nm
B. 182nm
C. 91nm
D. 273nm
E. 415nm

Answer 1

Hint: Recall the condition for constructive interference. Also note that the wavelength in the condition is that of the film. We know that the frequency doesn’t change while moving from one medium to another, also substitute for velocity in terms of refractive index and then you could get the wavelength of the light ray in film in terms of the given quantities. Considering nearly normal incidence, we get the path difference as twice the thickness of film. Equating this in the above condition gets you the thickness of film.

Formula used:
Condition for constructive interference,
$\Delta x=0,2\lambda ,3\lambda ,...,m\lambda $
Condition for destructive interference,
$\Delta x=\dfrac{\lambda }{2},\dfrac{3\lambda }{2},\dfrac{5\lambda }{2},...,\left( m+\dfrac{1}{2} \right)\lambda $
Expression for frequency,
$f=\dfrac{v}{\lambda }$
Expression for refractive index,
$n=\dfrac{c}{v}$

Complete step by step answer:
We are coating a thin film of refractive index 1.50 over a glass lens of refractive index 1.60. We are asked to find the thickness of the thinnest coating of the film that will cause constructive thin film interference for a very strongly reflected light of wavelength 546nm.
Let us discuss the thin film interference in a general case,

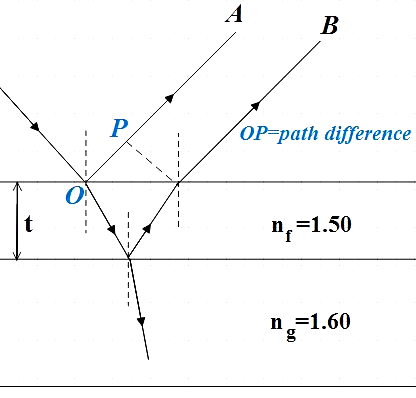
Recall that when a light travels from rarer medium to denser medium it suffers from a π- phase shift. Here the given system consists of two interfaces, first between air and the film and the second between the film and the glass. Since both these interfaces are from rarer to denser medium the light ray gets π shifted at both the interfaces. Therefore ray A as well as B are π shifted here, so the path difference is given by,
For constructive interference,
$\Delta x=0,2\lambda ,3\lambda ,...,m\lambda $ ………………………… (1)
For destructive interference,
$\Delta x=\dfrac{\lambda }{2},\dfrac{3\lambda }{2},\dfrac{5\lambda }{2},...,\left( m+\dfrac{1}{2} \right)\lambda $ …………………………… (2)
Path difference is clearly shown in the figure as OP, and for nearly normal incidence the path difference is twice the thickness of the film. That is,
$\Delta x=2t$ ………………………. (3)
Also, rays A as well as B has the same frequency (depends only on the source),
${{f}_{A}}={{f}_{B}}$
$\Rightarrow \dfrac{{{v}_{A}}}{{{\lambda }_{A}}}=\dfrac{{{v}_{B}}}{{{\lambda }_{B}}}$ ………………………. (4)
Where, ${{v}_{A}}$ and ${{v}_{B}}$ are the velocities, ${{\lambda }_{A}}$ and ${{\lambda }_{B}}$ are the wavelengths of ray A and B respectively.
But, refractive index is given by,
$n=\dfrac{c}{v}$
Now (4) becomes,
$\Rightarrow \dfrac{\dfrac{c}{{{n}_{A}}}}{{{\lambda }_{A}}}=\dfrac{\dfrac{c}{{{n}_{B}}}}{{{\lambda }_{B}}}$
$\Rightarrow {{\lambda }_{B}}=\dfrac{{{n}_{A}}}{{{n}_{B}}}{{\lambda }_{A}}$ …………………….. (5)
For constructive interference,
$\Delta x=m\lambda $
From (3),
$2t=m{{\lambda }_{B}}$
From (5),
$\Rightarrow 2t=m\left( \dfrac{{{n}_{A}}}{{{n}_{B}}}{{\lambda }_{A}} \right)$
For minimum thickness of film m=1, also,
${{n}_{A}}=1$
${{n}_{B}}=1.50$
${{\lambda }_{A}}=546nm$
$\Rightarrow 2t=1\times \left( \dfrac{1}{1.5}\times 546nm \right)$
$\Rightarrow t=\dfrac{546}{1.5\times 2}nm$
$\Rightarrow t=182nm$
Therefore, the thinnest coating of film that will provide constructive thin film interference for very strongly reflected 546nm light is t=182nm.

So, the correct answer is “Option B”.

Note: The conditions for constructive and destructive interference given in (1) and (2) are based on the fact that both rays A and B are suffering from a π phase shift. That is, there is no relative π shift between the two rays. If there exists a relative π shift between the two rays, the conditions for constructive and destructive interference gets interchanged.