Question

A thin film of liquid polymer, $n = 1.25$ coats a slab of Pyrex, $n = 1.50$. White light is incident perpendicularly on the film. In the reflection, full destructive interference occurs for $\lambda = 600\,nm$ and full constructive interference occurs for $\lambda = 700\,nm$. What is the thickness of the polymer film?

(A) $120\,nm$
(B) $280\,nm$
(C) $460\,nm$
(D) $840\,nm$

Answer 1

Hint: This problem is related to thin film interference, if the light is incident from one medium to another medium, the reflection is full destructive interference will occur at $\lambda = 600\,nm$ and the full constructive interference occurs for $\lambda = 700\,nm$, then the thickness of the film is determined by using the thin film interference formula.

Formulae Used:
By thin film interference, the thickness of the film is given by,
For constructive interference,
$2t = \dfrac{{m\lambda }}{n}$
Where, $t$ is the thickness of the film, $m$ is the order of the interference, $\lambda $ is the wavelength for constructive interference and $n$ is the refractive index.

Complete step-by-step solution:
Given that,
Refractive index of liquid polymer, ${n_1} = 1.25$
Refractive index of slab of Pyrex, ${n_2} = 1.50$
Wavelength for destructive interference, ${\lambda _1} = 600\,nm$
Wavelength for constructive interference, ${\lambda _2} = 700\,nm$

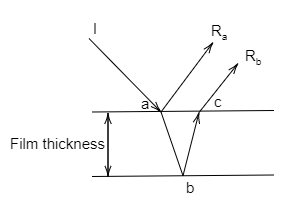
Thin-film interference is the interference of light waves reflecting off the top surface of a film with the waves reflecting from the bottom surface.
By thin film interference, the thickness of the film is given by,
For constructive interference,
$2t = \dfrac{{m{\lambda _2}}}{{{n_1}}}\,..................\left( 1 \right)$
For constructive interference, the wavelength is ${\lambda _2}$ and we have to find the thickness of the polymer film, so take the refractive index of polymer ${n_1}$.
By substituting the wavelength and refractive index value in the equation (1), then
$2t = \dfrac{{m \times 700}}{{1.25}}$
Here, $m$ is the order of interference, so take $m = 3$, and substitute in the above equation, then
$2t = \dfrac{{3 \times 700}}{{1.25}}$
On multiplying the numerator in the above equation, then
$2t = \dfrac{{2100}}{{1.25}}$
Now dividing the RHS, then the above equation is written as,
$2t = 1680$
By keeping the term $t$ in one side and the other terms in other side, then
$t = \dfrac{{1680}}{2}$
By dividing the terms, then
$t = 840\,nm$
Thus, the above equation shows the thickness of the polymer film.
Hence, the option (D) is the correct answer.

Note:- The thickness of the thin film is also determined by using the thin film interference formula for destructive interference. And the formula for destructive interference is $2t = \left( {m + \dfrac{1}{2}} \right)\left( {\dfrac{\lambda }{n}} \right)$ by using this formula the thickness of the thin film can be determined.