Question

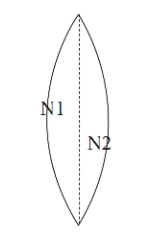
A thin convex lens is made of two materials with refractive indices ${{n}_{1}},{{n}_{2}}$ ​, as shown in figure. The radius of curvature of the left and right spherical surfaces are equal. F is the focal length of the lens when ${{n}_{1}}={{n}_{2}}=n$. The focal length is $f+\Delta f$ when ${{n}_{1}}=n$ and ${{n}_{2}}=n+\Delta n$. Assuming $\Delta n<<(n-1),(1

A) $\begin{align}
  & \dfrac{\Delta n}{n}<0,\dfrac{\Delta f}{f}>0 \\
 & \\
\end{align}$
B) for $n=1.5,\Delta n={{10}^{-3}},f=20cm$, the value of $\Delta f$will be 0.02cm.
C) \[|\dfrac{\Delta f}{f}|<|\dfrac{\Delta n}{n}|\]
D) the relation between $\dfrac{\Delta f}{f},\dfrac{\Delta n}{n}$remains unchanged if both the convex surfaces are replaced by concave surfaces of same radius of curvature.

Answer 1

Hint: The diversifying nature increases when the uncertainty in the refractive index decreases. The diversifying nature is directly proportional to the uncertainty in the focal length. Next, when a concave lens is updated with a convex lens or vice versa, the sign of the quantities like focal length, object distance and image distance changes, but the magnitude remains the same, meaning the uncertainties don't change.

Complete answer:
We know, using the lens makers formula, we can figure out the relation among focal length, refractive index and the radius of curvature.
\[\begin{align}
  & \dfrac{1}{f}=({{n}_{1}}-1)(\dfrac{1}{R}-\dfrac{1}{\propto })+({{n}_{2}}-1)(\dfrac{1}{\propto }-\dfrac{1}{-R}) \\
 & \Rightarrow \dfrac{1}{f}=\dfrac{({{n}_{1}}-1)}{R}+\dfrac{({{n}_{2}}-1)}{R} \\
 & \Rightarrow \dfrac{1}{f}=\dfrac{({{n}_{1}}+{{n}_{2}}-2)}{R} \\
\end{align}\]
Now, let us calculate the uncertainty,
$\begin{align}
  & \dfrac{\Delta f}{f}=\dfrac{\Delta n}{R} \\
 & \Rightarrow \dfrac{\Delta f}{f}=\dfrac{\Delta n}{({{n}_{1}}+{{n}_{2}}-2)} \\
 & \Rightarrow \dfrac{\Delta f}{f}=\dfrac{\Delta n}{(2n+\Delta n-2)} \\
\end{align}$
For the given values
$\begin{align}
  & {{n}_{1}}={{n}_{2}}=1.5 \\
 & \Delta n={{10}^{-3}},f=20cm \\
 & \Delta f=\dfrac{{{10}^{-3}}\times 20}{(2\times 1.5-2\times {{10}^{-3}})}=0.02cm \\
\end{align}$
Next,
If $\begin{align}
  & \dfrac{\Delta n}{n}<0, \\
 & \Rightarrow \dfrac{\Delta f}{f}>0 \\
\end{align}$as diversifying nature increases.
If the surfaces are replaced by concave surfaces of the same radius, the focal length and the uncertainty in the focal length doesn’t change as the signs of the quantities change but not the values.

Therefore, the correct options are a, b and d.

Additional information:
Refractive Index (Index of Refraction) is a value calculated from the ratio of the speed of light in a vacuum to that in a second medium of greater density. The refractive index variable is most commonly symbolized by the letter n or n' in descriptive text and mathematical equations. N optical microscopy, refractive index is an important variable in calculating numerical aperture, which is a measure of the light-gathering and resolving power of an object. In most instances, the imaging medium for microscopy is air, but high-magnification objectives often employ oil or a similar liquid between the objective front lens and the specimen to improve resolution.

Note:
When we change the reflecting or refracting material from a system and replace them with the other elms or mirror but with the same focal length, the signs of quantities such as focal length, object distance, height and image distance changes but the value remains the same.