Question

A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 3.5 m and 2 m respectively, and the slant height of the top is 3.5 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs.1000 per${m^2}$ (Note that the base of the tent will not be covered with canvas)

Answer 1

Hint: To solve this question, we need to know the basics theory related to the surface area of a cone and cylinder. Here, first we calculate Curved Surface area of Cone and then after also find Curved Surface area of Cylinder. And finally, we get the Area of Canvas, which is basically the sum of the curved area of Cone and curved surface area of the Cylinder.

Complete step-by-step answer:

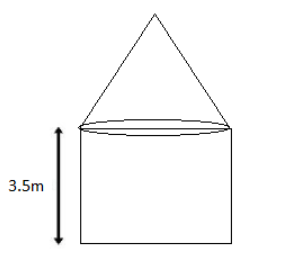
Area of Canvas = Curved Area of Cone + Curved Surface Area of the Cylinder
Let’s calculate the Curved Surface area of Cone:
Diameter of cone=Diameter of Cylinder=4 m
⟹radius = $\dfrac{4}{2}$= 2 m
Slant height=l=2.8 m
Curved Surface area of Cone = πrl
 = $\dfrac{{22}}{7}$×2×2.8=17.6 ${m^2}$
Curved Surface area of Cylinder=2πrh
= $2 \times \dfrac{{22}}{7} \times $2 $ \times $2.1= 26.4 ${m^2}$
∴The Area of Canvas=17.6+26.4=44 ${m^2}$
Now,
Cost of the canvas of the tent for 1 ${m^2}$ =Rs 500
Cost of the canvas of the tent for 44 ${m^2}$= 500×44 = Rs 22000
∴ Total Cost=22000 rupees
Therefore, 22000 rupees is the cost of the canvas of the tent at the rate of Rs. 1000 per ${m^2}$ .

Note: The formula for the surface area and volume of the cone is derived based on its height(h), radius(r) and slant height(l). Therefore, here we need to focus more on what is slant height?
The slant height of the cone (specifically right circular) is the distance from the vertex or apex to the point on the outer line of the circular base of the cone. The formula for slant height can be derived by the Pythagoras Theorem.
Slant Height, l = $\sqrt {{{\left( r \right)}^2} + {{\left( l \right)}^2}} $