Question

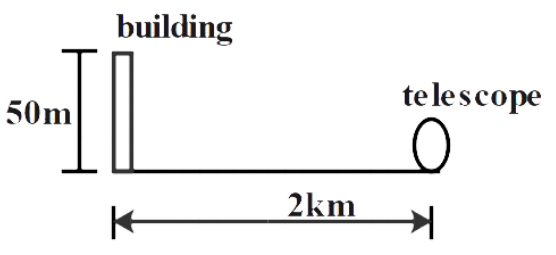
A telescope has an objective lens of focal length 200 cm and an eyepiece with focal length 2 cm. It is used to see a building of 50 m at a distance of 2 km. What is the height of the image formed by the objective lens?
A. 5 cm
B. 10 cm
C. 1 cm
D. 2 cm

Answer 1

Hint: In this question, we are asked to calculate the height of image formed by the objective lens. We know that the height of an image can be formed by using a magnification formula. It gives the relation between object height and image height with object distance and image distance. Therefore, we shall first calculate the image distance. That can be done using lens formula.

Formula used: \[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]
\[\dfrac{v}{u}=\dfrac{I}{O}\]
Where,
V is the image distance
U is the object distance
I is the image height
And, O is the object height

Complete step by step answer:
We shall first calculate the image distance

From lens formula
We know,
\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]
It is given that focal length of objective lens is 200 cm and the building is 2 km away (2 km= 2000 m)
After substituting values
We get,
\[\dfrac{1}{v}=\dfrac{1}{2}-\dfrac{1}{2000}\]
Therefore,
\[v=\dfrac{2000}{999}m\]
Now, from magnification formula
We know,
\[\dfrac{v}{u}=\dfrac{I}{O}\]
After substituting values
We get,
\[\dfrac{2000}{999\times 2000}=\dfrac{I}{50}\]
Therefore,
\[I\approx 0.05m\]
Therefore,
\[I\approx 5cm\]
This approximation is required because we can assume that the object is placed at infinite distance.
So, the correct answer is “Option A”.

Note: Magnification refers to an action of visually enlarging the image with the help of lenses. The object does not physically become larger, it appears to be large. The formula of magnification represents the ratio of height of image to the height of object. The lens formula or mirror formula is the equation relating the image distance and object distance to the focal length.