Question

A swimming pool is \[18m\] long and \[8m\] wide. Its deep and shallow ends are \[2m\] and \[1.2m\] respectively. Find the capacity of the pool assuming that the bottom of the pool slopes uniformly.
A. \[230.4cu.m\]
B. \[420.4cu.m\]
C. \[340.4cu.m\]
D. \[190.4cu.m\]

Answer 1

Hint: To find the capacity of the pool, we will first draw a diagram based on the above given measurements. The shape of the pool is similar to trapezoid prism. We will first find the area of the trapezium and then multiply it with the distance between the two trapezoidal faces as a result we will get the volume of the pool or we can say, the capacity of the pool.

Complete step by step solution:
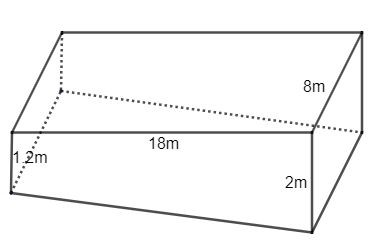
According to the question given, we have a pool which has a rectangular surface and the bottom varies in depth from \[1.2m\] to \[2m\] which slopes gradually, so the lateral shape of the pool is a trapezoid.
The capacity of the pool which is a trapezoid prism = Base area of the trapezium \[\times \] height (distance between the two trapezoid face)
The pool looks like this, having trapezium face on the two lateral sides.
   

First, we will find the area of the trapezoid face, and for that we will focus on the marked faces, which is,

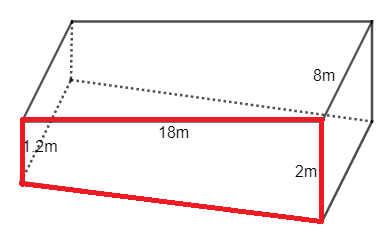
We know that, \[Area\_of\_trapezium=\dfrac{1}{2}({{B}_{1}}+{{B}_{2}})\times h\]
Where \[{{B}_{1}}\] and \[{{B}_{2}}\] are the length of sides which are parallel to each other.
\[h\] is the height or the distance between the two parallel sides.
From the figure, we get,
\[{{B}_{1}}=1.2m\]
\[{{B}_{2}}=2m\]
\[h=18m\]
Substituting the values in the area of the trapezium, we get,
\[Area\_of\_trapezium=\dfrac{1}{2}({{B}_{1}}+{{B}_{2}})\times h\]
\[=\dfrac{1}{2}(1.2+2)\times 18\]
\[=\dfrac{1}{2}(3.2)\times 18=(3.2)\times 9\]
\[=28.8{{m}^{2}}\]
We have found the area of trapezium on one side, but there are two trapezoid sides which are separated by a distance of \[8m\], so we just need to multiply this distance to the area we got, in order to obtain the capacity of the pool.
The capacity of the pool which is a trapezoid prism = Base area of the trapezium \[\times \] height
\[=28.8{{m}^{2}}\times 8m\]
\[=230.4{{m}^{3}}\]
Therefore, the capacity of the pool is (A) \[230.4cu.m\]
So, the correct answer is “Option A”.

Note: The trapezoid prism is a 3D representation of the 2D trapezium. In 3D representation, an additional distance comes into picture and only after multiplying this factor with the area of the trapezium can the capacity or the volume be determined. While dealing questions with trapezoid figures, diagrams are advisory to get a better picture of the given conditions.