Question

A student used to go to his coaching institute every evening and he takes 20 min. Once on his way, he realized that he had forgotten his book at home. He knew if he continued walking at the same speed, he would be there 8 min before the bell, so he went back home for the book and arrived the coaching 10 min late, if he had walked all the way with his usual speed, the fraction of the way to coaching institute had he covered at that moment when he turned back is x/20. Find the value of x.

Answer 1

Hint: We can solve this question by using following formula: speed to directly proportional to distance and inversely proportional to time, hence, $ speed=\dfrac{dis\tan ce}{time} $ .or
Distance = speed $ \times $ time
As the speed increases the time taken will decrease and vice versa.

Complete step by step solution
We have given Case I: A student used to go to his coaching institute every evening and he takes 20 min. We use, the formula, $ velocity=\dfrac{dis\tan ce}{time} $

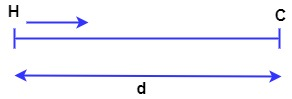
Let d is the distance from home to coaching. If he walks from home to coaching
Time taken = 20min
Then speed = $ \dfrac{d}{20} $ --------- (1)
Let x is the distance from home to the turning point on the day he forgot his book at home. On that day, total distance travelled $ =\text{d}+\text{x }+\text{x} $
 $ =\text{2x}+\text{d} $

Since normally he reaches 8min before the bell ringing time, but on that day he reached 10 min after the bell.
Total time taken $ =\text{ 2}0+\text{8}+\text{1}0=38 $ min
 $ velocity=\dfrac{2x+d}{38} $ . ----------(2)
 From eq. (1)and (2)
 $ \dfrac{d}{20}=\dfrac{2x+d}{38} $
 $ \dfrac{38}{20}=\dfrac{2x+d}{d} $
 $ \dfrac{2x+d}{d}=\dfrac{19}{10} $
 $ 2\left( \dfrac{x}{d} \right)+1=\dfrac{19}{10} $
 $ 2\left( \dfrac{x}{d} \right)=\dfrac{19}{10}-1 $
 $ 2\left( \dfrac{x}{d} \right)=\dfrac{9}{10} $
 $ \dfrac{x}{d}=\dfrac{9}{20}\Rightarrow x=\dfrac{9}{20}d $
Hence, we get the required fraction x/d from the above equation.
 $ \dfrac{x}{d}=\dfrac{9}{20} $

Note
If two bodies move at the same speed, the distance covered by them is directly proportional to time taken i.e., v is constant.
If two bodies move the same time period, then the distance covered by them is (directly). Proportional to the speed of travel i.e., t is constant.
If two bodies move for the same distance, their time of travel is inversely proportional to the speeds of travel i.e., d is constant.