Question

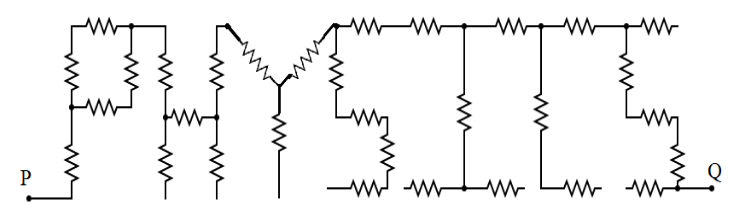
A student of Narayana e-techno school connected 31 resistors of equal resistance $R$ to form the word PHYSICS. What will be the effective resistance between $P$ and $Q$ ?

A. $12R$
B. $13R$
C. $14R$
D. $15R$

Answer 1

Hint: The answer to the problem requires us to find which resistances are connected in series and which are connected in parallel. The formula for the resistances in series and parallel is applied in order to find the equivalent resistance. The answer relates to determining a path from the point $P$ to point $Q$ and the number of resistors connected in series or parallel to each other.

Formula used:
The resistances in series are given by the equation:
${R_s} = {R_1} + {R_2} + {R_3} + .... + {R_n}$
The resistances in parallel are given by the equation:
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ....\dfrac{1}{{{R_n}}}$

Complete step by step answer:
A complex circuit with a lot of resistors connected to it can be easily solved by reducing the circuit. The question asks us to find out the value of the equivalent resistance or the effective value of the resistance which is the total resistance offered by that path. In order to find this out we must create a path from point $P$ to point $Q$.

The path should be constructed in such a way that all the wires are connected and there are no sudden gaps or disconnections in the path. A single route must be determined and this route which consists of a certain number of resistors will be reduced using the series or parallel resistances formula.

As our first step, let us first determine a path from point $P$ to $Q$ which connects all the resistors present in that path. The diagram below illustrates the path that is to be taken:

Since only a single path is to be considered connecting terminals $P$ and $Q$ the other resistors which do not come in this path are omitted and their resistance value is not to be included in our calculation.

Let us now look at the concept of resistances in series and resistances in parallel.The resistances in series equation states that if a number of resistances are connected in series then their equivalent that is the net resistance will be the sum of the individual resistances.This is given by the equation:
${R_s} = {R_1} + {R_2} + {R_3} + .... + {R_n}$ ------($1$)

When two or more resistances are connected in between two common points they are said to be connected in parallel to each other, that is, when the resistors have a common junction or a separate wire which connects both of them. The resistances in parallel equation states that when a number of resistances are connected in parallel then their equivalent, that is, the net resistance will be the sum of the reciprocals of their individual resistances.This is given by the equation:
$\dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ....\dfrac{1}{{{R_n}}}$

The formula for two resistances in parallel derived from the above equation is given by:
${R_{eq}} = \dfrac{{{R_1} \times {R_2}}}{{{R_1} + {R_2}}}$ ------($2$)
Since we are asked to find the equivalent resistance, we use a property wherein a combination of two or more resistances which are connected in series or parallel are replaced by a single resistance value and this is known as reducing the circuit into a much more simpler circuit.

Let us look at the resistances connected to form a part of the letter $P$ more closely.

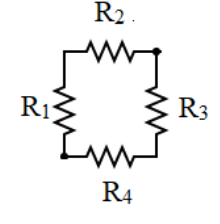
As we can see, the resistances ${R_1}$ and ${R_2}$ are connected in series to each other and the resistances ${R_3}$ and ${R_4}$ are connected in series to each other since they are connected by a single wire. However the resistances ${R_1}$ and ${R_2}$ are connected in parallel to the resistances ${R_3}$ and ${R_4}$ since they are connected by a different wire creating junctions.

All the resistances of the circuit are given to be equal in magnitude and are given by the value $R$.Since, ${R_1}$ and ${R_2}$ are in series from equation ($1$) we get:
${R_{eq1}} = {R_1} + {R_2}$
$ \Rightarrow {R_{eq1}} = R + R = 2R$
Since, ${R_3}$ and ${R_4}$ are in series
${R_{eq2}} = {R_3} + {R_4}$
$ \Rightarrow {R_{eq2}} = R + R = 2R$
The resistors ${R_{eq1}}$ and ${R_{eq2}}$ are said to be in parallel to each other.
Hence by the formula from equation ($2$),
${R_{eq}} = \dfrac{{{R_{eq1}} \times {R_{eq2}}}}{{{R_{eq1}} + {R_{eq2}}}}$
$ \Rightarrow {R_{eq}} = \dfrac{{2R \times 2R}}{{2R + 2R}}$
$ \Rightarrow {R_{eq}} = \dfrac{{4{R^2}}}{{4R}}$
${R_{eq}} = R$ ------($3$)
Hence the circuit is reduced as shown in the diagram below omitting all the resistors that are not included in our path.

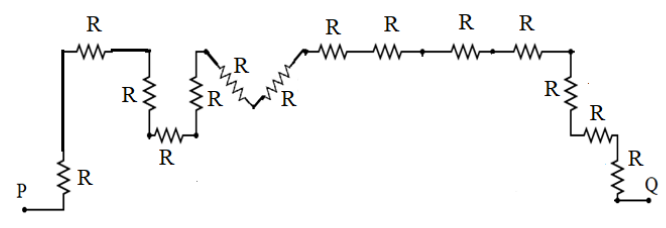
From our path we can say that all the other resistances which are included in our path are said to be connected in series to each other as all of them are connected via a single wire without any separate junctions between them.

Hence, as per the circuit diagram we can see that there are $14$ resistors connected together including the resistor from the equation ($3$). Therefore we apply the formula from equation ($1$) and the $n$ value is said to be $14$. So putting $n = 14$ equation ($1$) becomes:
${R_s} = {R_1} + {R_2} + {R_3} + .... + {R_{14}}$
Since all the resistances have a value of $R$ we get:
${R_s} = R + R + R + .... + R$
$ \therefore {R_s} = 14R$

Therefore, This is the effective resistance of the circuit is $14R$. So, the correct option is option (C).

Note: The simplest path from the given points is supposed to be found out since the current always has a tendency to flow through the path with the least amount of resistance. All the $31$ resistors may not be used in the path from the $P$ to $Q$. Some resistors may be omitted which can be seen in the above solution of the problem.