Question

A steel wire 1.5 m long and of radius 1 mm is attached with a load 3 kg at one end. The other end of the wire is fixed. It is whirled in a vertical circle with a frequency 2 Hz. Find the elongation of the wire when the weight is at lowest position: (Y = $2\times {{10}^{11}}N/{{m}^{2}}$and g = $10m/{{s}^{2}}$)
A. $1.77\times {{10}^{-3}}m$
B. $7.17\times {{10}^{-3}}m$
C. $3.17\times {{10}^{-3}}m$
D. $1.37\times {{10}^{-3}}m$

Answer 1

Hint: We will be analysing the forces acting on the wire which will be a combination of the mass of the load and the tension on the wire which provides the necessary centripetal force for the circular motion. And then we will calculate the elongation of wire due to the forces acting on it, using the young’s modulus formula.

Formula used:
Young’s modulus
$Y=\dfrac{\left( \dfrac{F}{A} \right)}{\left( \dfrac{\Delta L}{L} \right)}=\dfrac{FL}{A\Delta L}$

Complete step by step answer:
We will take some assumptions to solve this question. We will assume that there is no effect of gravity on the angular velocity of the load. This is taken to make the problem solving easy because assuming the effect of gravity would make it a very high-level mathematical problem, which we don’t want. Now we are given that the frequency of circular motion is 2 Hz, then the angular velocity will be equal to
$\omega =2\pi \nu =2\pi \times 2=4\pi $
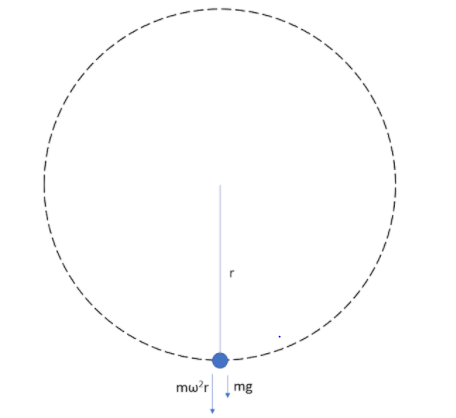
Then we can find the centripetal force needed to keep the load moving in the circle which will also be equal to the tension in the wire that keeps the load moving in the circle.
${{F}_{centripetal}}=m{{\omega }^{2}}r=3\times {{\left( 4\pi \right)}^{2}}\times 1.5=710.6$N
And now the force due to the weight of the load
${{F}_{load}}=mg=3\times 10=30$N
Total force on the wire will be
$F={{F}_{load}}+{{F}_{centripetal}}=30+710.6=740.6$N

Using the formula for Young’s modulus we get elongation as
$Y=\dfrac{FL}{A\Delta L}\Rightarrow \Delta L=\dfrac{FL}{AY}$
Putting in the values we get
$\Delta L=\dfrac{FL}{AY}=\dfrac{740.6\times 1.5}{\pi \times {{\left( {{10}^{-3}} \right)}^{2}}\times 2\times {{10}^{11}}}=1.77\times {{10}^{-3}}$m
Hence, the correct option is A, i.e. $1.77\times {{10}^{-3}}m$.

Note:
We can find the kinetic energy of the load at the lowest point and also the change in potential energy when the load reaches the top, we will see that the difference is huge, that’s why we ignore the effect of gravity on the singular velocity. If both were comparable to each other then we would have to take the effect of gravity in consideration.