Question

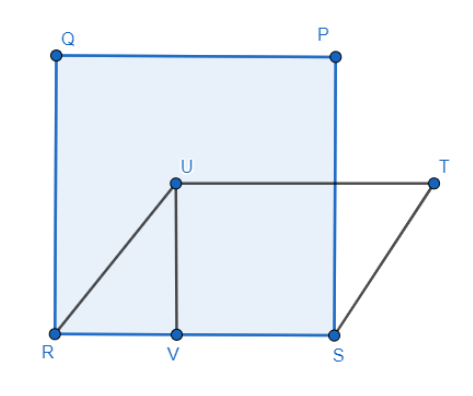
A square PQRS and a rhombus RSTU lie on the same base RS. What is the relation between their areas?

A. \[ar\left( PQRS \right)=ar\left( RSTU \right)\]
B. \[ar\left( PQRS \right) < ar\left( RSTU \right)\]
C. \[ar\left( PQRS \right) > ar\left( RSTU \right)\]
D. \[ar\left( PQRS \right)=\dfrac{1}{2}ar\left( RSTU \right)\]

Answer 1

Hint: We find the formula of finding the area of \[ar\left( PQRS \right)\] and \[ar\left( RSTU \right)\]. We compare their heights and find a relation. This gives the relation between the area of the square and the rhombus when multiplied by the length of the common base RS.

Complete step by step solution:
A square PQRS and a rhombus RSTU lie on the same base RS.
We know the formulas to find the areas for square and rhombus.
For square it is the square value of one side and for rhombus it is the multiplication of one side and the height.
For square PQRS, we find the area with respect to the sides’ length.
So, \[ar\left( PQRS \right)=RS\times PS\]. Both are sides of the square.
We take the intersection of PS and UT as a point of O.

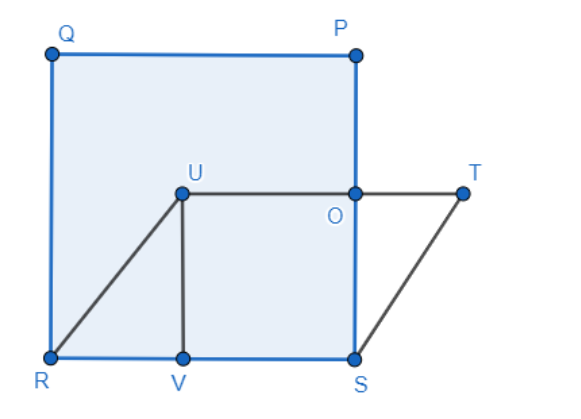
We now try to prove that quadrilateral UVSO is a square.
We know that $\angle UVR=\angle UVS=\angle OSV={{90}^{\circ }}$. Therefore, $UV||OS$.
Also, as RSTU is a rhombus we have $UT||RS$ which gives $UO||VS$.
Therefore, UVSO is a square for having opposite sides as parallel and all angles being equal to ${{90}^{\circ }}$. This gives $UV=OS$. These lines become the height of the rhombus.
The area of the rhombus becomes \[ar\left( RSTU \right)=RS\times OS\].
We can clearly see that $OS < PS$. Therefore, $RS\times OS < RS\times PS$.
This gives \[ar\left( PQRS \right) > ar\left( RSTU \right)\]. The correct option is C.
So, the correct answer is “Option C”.

Note: We need to be careful about the proof of the parallelogram. The proof gives us a relation between the heights. The height for the square is the side as that creates the right angle on the base.