Question

A square of side \[\sqrt{2}m\]has charges of \[+2\times {{10}^{-9}}C\],\[+1\times {{10}^{-9}}C\],\[-2\times {{10}^{-9}}C\]and \[-3\times {{10}^{-9}}C\]respectively at its corners. What is the potential at the centre of the square?
A. +8V
B. -8V
C. +18V
D. -18V

Answer 1

Hint: The resulting potential at any point is due to all the charge creating electric potential at the point. And that resulting potential is the sum of the potentials of all the individual charges. And the formula for potential due to point charge is given below.

Formula used: \[V=\dfrac{kq}{r}\]

Complete step by step answer:
The resulting potential at any point is due to all the charge creating electric potential at the point. And that resulting potential is the sum of the potentials of all the individual charges.
The potential at a point due to a charge ‘q’ at a distance ‘r’ is given by
\[V=\dfrac{kq}{r}\]
Here k is the Coulomb's law constant and it is equal to
\[\begin{align}
  & k=\dfrac{1}{4\pi {{\in }_{0}}} \\
 & k=9\times {{10}^{9}}N{{m}^{2}}/{{C}^{2}} \\
\end{align}\]
Coming to the question, the charges are placed at the corner of the square of side \[\sqrt{2}m\]and we have to find the total potential at the centre of the square.

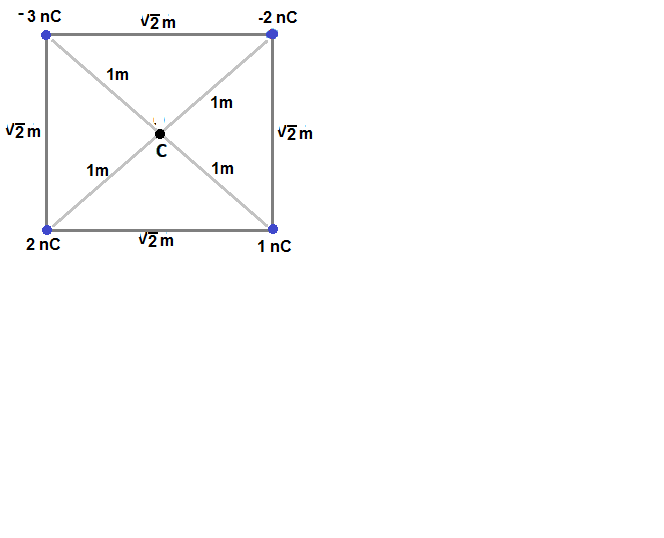
The distance between the corner and centre of a square of side ‘a’ is
\[\dfrac{a}{\sqrt{2}}\]
The given square has a side length of \[\sqrt{2}m\]. So, the distance between the corner and centre of a square is
\[\dfrac{\sqrt{2}}{\sqrt{2}}=1m\]
Now Let the Charges at the corner be \[{{q}_{_{1}}}\] \[{{q}_{2}}\] \[{{q}_{3}}\]and \[{{q}_{4}}\]. And their individual potentials at the centre be \[{{V}_{1}}\] \[{{V}_{2}}\] \[{{V}_{3}}\]and \[{{V}_{4}}\] respectively
We also know that potential at a point due to a charge ‘q’ at a distance ‘r’ is given by
\[V=\dfrac{kq}{r}\]
Plugging in Values of each charge we get
\[\begin{align}
  & {{V}_{1}}=\dfrac{k{{q}_{_{1}}}}{{{r}_{1}}} \\
 & \Rightarrow {{V}_{1}}=\dfrac{k\times 2\times {{10}^{-9}}}{1} \\
\end{align}\]
For \[{{q}_{2}}\]
\[\begin{align}
  & {{V}_{2}}=\dfrac{k{{q}_{2}}}{{{r}_{2}}} \\
 & \Rightarrow {{V}_{2}}=\dfrac{k\times 1\times {{10}^{-9}}}{1} \\
\end{align}\]
For \[{{q}_{3}}\]
\[\begin{align}
  & {{V}_{3}}=\dfrac{k{{q}_{3}}}{{{r}_{3}}} \\
 & \Rightarrow {{V}_{3}}=\dfrac{k\times (-2\times {{10}^{-9}})}{1} \\
\end{align}\]
And For \[{{q}_{4}}\]
\[\begin{align}
  & {{V}_{4}}=\dfrac{k{{q}_{4}}}{{{r}_{4}}} \\
 & \Rightarrow {{V}_{4}}=\dfrac{k\times (-3\times {{10}^{-9}})}{1} \\
\end{align}\]
Now the total potential at the centre ‘\[{{V}_{c}}\]’ will be the sum of all the potentials due to individual charges
So,
 \[\begin{align}
  & {{V}_{c}}={{V}_{1}}+{{V}_{2}}+{{V}_{3}}+{{V}_{4}} \\
 & \Rightarrow {{V}_{c}}=\dfrac{k\times 2\times {{10}^{-9}}}{1}+\dfrac{k\times 1\times {{10}^{-9}}}{1}+\dfrac{k\times (-2\times {{10}^{-9}})}{1}+\dfrac{k\times (-3\times {{10}^{-9}})}{1} \\
 & \Rightarrow {{V}_{c}}=\left( k\times {{10}^{-9}} \right)\times \left( 2+1-2-3 \right) \\
 & \Rightarrow {{V}_{c}}=\left( 9\times {{10}^{9}}\times {{10}^{-9}} \right)\times \left( -2 \right) \\
 & \Rightarrow {{V}_{c}}=9\times \left( -2 \right) \\
 & \Rightarrow {{V}_{c}}=\left( -18 \right)V \\
\end{align}\]

So, the correct answer is “Option D”.

Note: Electric Potential is a Scalar quantity that means it has no direction. And thus the resulting potential at any point can be found by a simple arithmetic sum of all the individual potentials. Only distance between the charge and point is needed and no regard for the position of the individual charges is required.