Question

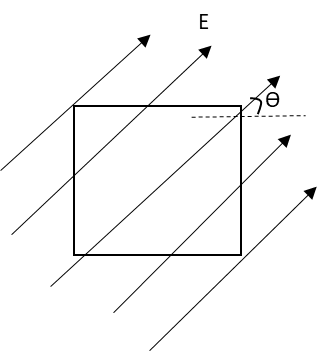
A square of side L meter in the plane of the paper is placed in a uniform electric field E(volt/m) acting along the same plane at an angle with the horizontal side of the square as shown in figure. The electric flux linked to the surface in units of \[{\text{volt - m}}\], is

A. \[E{L^2}\]
B. \[\cos^2 \theta \]
C. \[\sin^2 \theta \]
D. Zero

Answer 1

Hint: Use the formula for the electric flux linked with a surface. This formula gives the relation between the electric field vector, area vector of the surface and the angle between the electric field vector and area vector of the surface. Determine the angle between the electric field vector and area vector for the given square.

Formula used:
The flux of electric field through a surface is given by
\[\vec \phi = \vec E\vec A\cos \theta \] …… (1)
Here, \[\phi \] is the flux of electric field through the surface, \[\vec E\] is the electric field vector, \[\vec A\] is the area vector of the surface and \[\theta \] is the angle between the electric field vector and area vector of the surface.

Complete step by step answer:
We have given that the square is placed in the plane of paper and an uniform electric field \[E\] is passing though the same plane of paper making an angle \[\theta \] with the horizontal.
Suppose the square is placed in the X-Y plane.
The area vector of a surface is the vector which is in a perpendicular direction with the surface.
Hence, if the square is placed in the X-Y plane, the direction of the area vector \[\vec A\] of this surface will be in the Z-direction.
\[\vec A = A\hat k\]
The electric field is also in the same plane of the paper in which the square is placed. Hence, the electric field vector is also in X-Y direction.
\[\vec E = E\left( {\hat i + \hat j} \right)\]
Since the X, Y and Z directions are perpendicular to each other, the angle between Z-axis and X-Y axes is \[90^\circ \].
We can determine the flux linked with the given square surface using equation (1).
Substitute \[E\left( {\hat i + \hat j} \right)\] for \[\vec E\], \[A\hat k\] for \[\vec A\] and \[90^\circ \] for \[\theta \] in equation (1).
\[\vec \phi = \left[ {E\left( {\hat i + \hat j} \right)} \right]\left( {A\hat k} \right)\cos 90^\circ \]
\[ \Rightarrow \vec \phi = \left[ {E\left( {\hat i + \hat j} \right)} \right]\left( {A\hat k} \right)\left( 0 \right)\]
\[ \Rightarrow \vec \phi = 0\,{\text{V}} \cdot {\text{m}}\]
Therefore, the flux linked to the square surface in units of volt-m is zero.

So, the correct answer is “Option D”.

Note:
One can use another method for solving the same question. The electric flux is the number of lines passing through the given area. But in the present case the electric field and area of the surface are parallel, so no lines pass through the surface. Hence, the electric flux must be zero. The angle \[\theta \] in the diagram is different from the angle used in formula.