Question

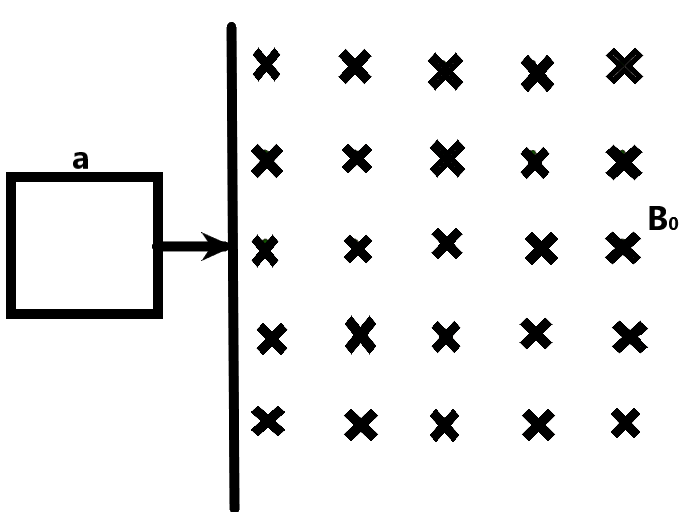
A square loop of side a, resistance R, mass m is sliding as shown on a smooth horizontal table with speed \[{{v}_{0}}\]. It enters a uniform magnetic field of magnitude \[{{B}_{0}}\] perpendicular to the table. It is seen that the loop comes to rest after entering a distance \[l\] inside the magnetic field. The value of \[{{v}_{0}}\] can be –

\[\begin{align}
  & \text{A) }\dfrac{{{B}^{2}}{{a}^{3}}}{mR} \\
 & \text{B) }\dfrac{{{B}^{2}}{{a}^{3}}}{2mR} \\
 & \text{C) }\dfrac{{{B}^{2}}{{a}^{3}}}{3mR} \\
 & \text{D) }\dfrac{{{B}^{2}}{{a}^{3}}}{6mR} \\
\end{align}\]

Answer 1

Hint: We need to understand the factors that are affecting the motion of a resistor in a perpendicular magnetic field. We can relate the given quantities such as the magnetic field, resistance, and area of the loop to get the velocity of the square initially.

Complete step-by-step solution
We know that the magnetic field provides a force on a conducting material, which moves in the field with a perpendicular component of velocity to the direction of the magnetic field. We are given a square, which moves with its plane perpendicular to the direction of the magnetic field with an initial velocity.
The Lorentz force due to this motion experienced by the square loop is given by –
 \[F=BlI\]
Where B is the magnetic field strength,
 \[l\] is the side of the square loop,
‘I’ is the induced current in the square loop.
 

We know that the current induced in a loop is given by the relation –
\[I=\dfrac{Ba{{v}_{0}}}{R}\]
Substituting this in the equation for force gives –
\[\begin{align}
  & I=\dfrac{Ba{{v}_{0}}}{R} \\
 & \Rightarrow F=Ba\dfrac{Ba{{v}_{0}}}{R} \\
 & \therefore F=\dfrac{{{B}^{2}}{{a}^{2}}{{v}_{0}}}{R} \\
\end{align}\]
We can equate the force to the product of the mass and acceleration on the square loop as –
\[\begin{align}
  & F=\dfrac{{{B}^{2}}{{a}^{2}}{{v}_{0}}}{R} \\
 & \Rightarrow m{{a}_{f}}=\dfrac{{{B}^{2}}{{a}^{2}}{{v}_{0}}}{R} \\
 & \Rightarrow -m\dfrac{d{{v}_{0}}}{dt}=\dfrac{{{B}^{2}}{{a}^{2}}{{v}_{0}}}{R} \\
 & \text{but,} \\
 & \dfrac{d{{v}_{0}}}{dt}={{v}_{0}}\dfrac{d{{v}_{0}}}{dx} \\
\end{align}\]
\[\begin{align}
& \Rightarrow -m{{v}_{0}}\dfrac{d{{v}_{0}}}{dx}=\dfrac{{{B}^{2}}{{a}^{2}}{{v}_{0}}}{R} \\
& \Rightarrow -m\int_{{{v}_{0}}}^{v}{d{{v}_{0}}}=\dfrac{{{B}^{2}}{{a}^{2}}}{R}\int_{0}^{x}{dx}\\
& \Rightarrow -m(v-{{v}_{0}})=\dfrac{{{B}^{2}}{{a}^{2}}x}{R} \\
& \Rightarrow v={{v}_{0}}-\dfrac{{{B}^{2}}{{a}^{2}}x}{mR} \\
& \text{but,} \\
& v=0,x=a \\
& \therefore {{v}_{0}}=\dfrac{{{B}^{2}}{{a}^{3}}}{mR} \\
\end{align}\]
This is the required initial velocity for the square to travel a distance of ‘l’ in the magnetic field.
The correct answer is option A.

Note: The moving coil or the square loop should have a perpendicular component along the direction of the magnetic field for any Lorentz force act upon the conducting coil or the resistor. We needn’t require the angle here because all the velocity was along the perpendicular.