Question

A spot of light S rotates in a horizontal plane with a constant angular velocity of 0.1rad/s. The spot of light P moves along the wall at a distance of 3m from S. The velocity of spot P, where \[\theta = 45^\circ \] , is?
A. $0.5m/s$
B. $0.6m/s$
C. $0.7m/s$
D. $0.8m/s$

Answer 1

Hint:-The formula for angular velocity is given by $\omega = \dfrac{{d\theta }}{{dt}}$ where $\theta $ is the angle between the perpendicular from the source to the wall and the line joining the source and the spot. For your better understanding a diagram is given for the situation.

Complete step-by-step solution:-
The situation in the question is given in the diagram for better understanding
 As given in the question that the perpendicular distance between the source and the wall, $SA = r = 3m$
Let angle between SA and SP be $\theta $ and the distance PA be $x$
Now, the velocity of the spot of light P, $v$ is the rate at which $x$ is changing i.e. $v = \dfrac{{dx}}{{dt}}$

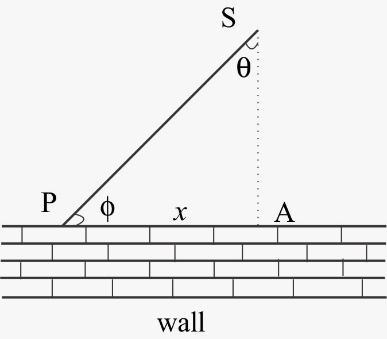
As from figure,
$x = r\tan \theta $
So, velocity of the point P
$v = \dfrac{{dx}}{{dt}} = r{\sec ^2}\theta \dfrac{{d\theta }}{{dt}}$
Now as we know that angular velocity is given by $\omega = \dfrac{{d\theta }}{{dt}}$ where $\theta $ is the angle between the perpendicular from the source to the wall and the line joining the source and the spot.
So, the equation becomes $v = r\omega {\sec ^2}\theta $
Now according to the question $\theta = 45^\circ $ , $r = 3m$ and angular velocity $\omega = 0.1rad/s$
So, substituting these value in the above equation, we have
$v = 3 \times 0.1 \times {\sec ^2}45^\circ = 3 \times 0.1 \times 2$
So, $v = 0.6m/s$

Hence option B is correct.

Note:- Angular velocity is the time rate of change of angular displacement at which an object or a particle is rotating around a center or a specific point. It is also known as rotational velocity. The unit of Angular velocity is angle per unit time or radians per second (rad/s). The rate of change of angular velocity is angular acceleration.
Angular velocity plays an important role in the rotational motion of an object. The linear velocity of every particle of a body in circular motion is directly related to the angular velocity of the whole object.