Question

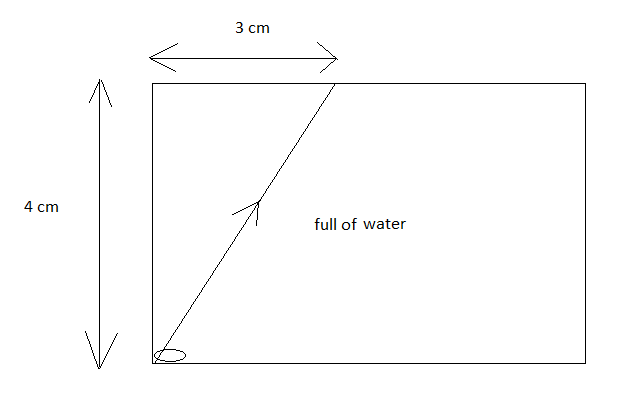
A small coin is resting on the bottom of a beaker filled with a liquid. A ray of light from the coin travels up to the surface of the liquid and moves along its surface (see figure)
How fast is the light travelling in the liquid?

A. \[3 \times {10^8}\,{\text{m/s}}\]
B. \[1.8 \times {10^8}\,{\text{m/s}}\]
C. \[2.4 \times {10^8}\,{\text{m/s}}\]
D. \[3.0 \times {10^8}\,{\text{m/s}}\]

Answer 1

Hint: First of all, we will draw the diagrams, for which it will become much easier. Then we will find out the refractive index of the liquid medium. After that using the refractive index and the velocity of light in air, we will find out the velocity of light in that medium.

Complete step by step answer:
In the given solution, we are supplied the following data:
A coin is placed at the bottom of a beaker.
The height of the liquid column is \[4\,{\text{cm}}\] .
We are asked to find the velocity of light in the liquid.

The critical angle is that angle of incidence in the denser medium for which the refracted ray emerges out at right angle in the lighter or rarer medium. For better understanding we draw a diagram.

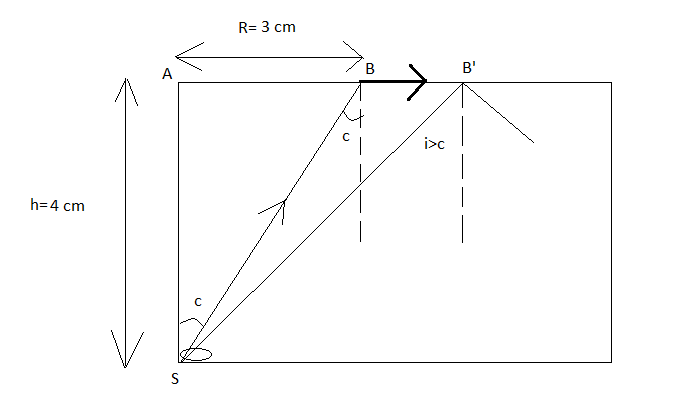
First, we will try to find out the refractive index of the liquid. Without finding the refractive index, we won’t be able to find the velocity of light in the liquid. From the diagram it is clear that angle \[C\] is the critical angle in the triangle \[SAB\]. The refracted ray will continue to emerge if the angle of incidence is equal to or less than the critical angle. However, if the angle of incidence is more than the critical angle, then the refracted ray will not emerge out of the liquid, rather it will be reflected back inside the liquid.
The minimum radial distance for which the angle of incidence is equal to the critical angle is \[R\] .
Now we apply a trigonometric ratio tangent in the triangle \[SAB\] .
\[\tan C = \dfrac{R}{h}\] …… (1)
Where,
\[R\] indicates the radial distance.
\[h\] indicates the height of the liquid column.

From equation (1), we can write:
\[R = h\tan C\] …… (2)

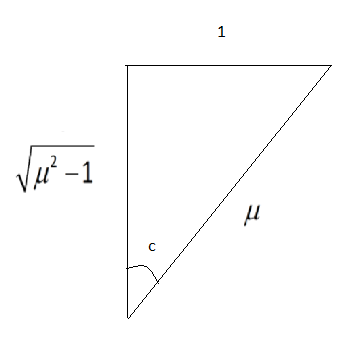
From the figure, we can write:
\[\tan C = \dfrac{1}{{\sqrt {{\mu ^2} - 1} }}\]

From equation (1), we get, by substituting the required values:
\[
\dfrac{1}{{\sqrt {{\mu ^2} - 1} }} = \dfrac{R}{h} \\
\Rightarrow \dfrac{1}{{\sqrt {{\mu ^2} - 1} }} = \dfrac{3}{4} \\
\Rightarrow \sqrt {{\mu ^2} - 1} =\dfrac{4}{3} \\
\Rightarrow {\mu ^2} - 1 = {\left( {\dfrac{4}{3}} \right)^2} \\
\]
Again, we simplify further, and we get:
\[
{\mu ^2} = \dfrac{{16}}{9} + 1 \\
\Rightarrow {\mu ^2} = \dfrac{{25}}{9} \\
\Rightarrow \mu =\dfrac{5}{3} \\
\Rightarrow \mu = 1.67 \\
\]
Therefore, the refractive index of the liquid is found to be \[1.67\] .

Now, we find the velocity of light by using refractive index by the formula:
\[\mu = \dfrac{c}{v}\] …… (3)
Where,
\[\mu \] indicates the refractive index of the liquid.
\[c\] indicates the velocity of light.
\[v\] indicates the velocity of light in the liquid medium.

Now, substituting the required values in the equation (3), we get:
\[
v = \dfrac{c}{\mu } \\
\Rightarrow v = \dfrac{{3 \times {{10}^8}\,{\text{m/s}}}}{{1.67}} \\
\Rightarrow v = 1.79 \times {10^8}\,{\text{m/s}} \\
\Rightarrow v \sim 1.8 \times {10^8}\,{\text{m/s}} \\
\]
Hence, the velocity of light in the liquid medium is \[1.8 \times {10^8}\,{\text{m/s}}\] .
The correct option is B.

Note:This problem can be solved if we have some knowledge of refraction of light. It is important to note that the refracted ray will not emerge out of the liquid if the angle of incidence is more than that of the critical angle. Critical angle is a specific property of a medium. Always remember that higher the magnitude of refractive index is, slower is the light travels in that particular medium or vice-versa.