Question

A small coil of radius r is placed at the center of a large coil of radius R, where R>>r. The two coils are coplanar. The mutual inductance between the coils is proportional to
A. \[\dfrac{r}{R}\]
B. \[\dfrac{{{r^2}}}{R}\]
C. \[\dfrac{{{r^2}}}{{{R^2}}}\]
D. \[\dfrac{r}{{{R^2}}}\]

Answer 1

Hint: When a current-carrying conductor is linked with another coil, then a voltage is induced in the second coil, and this phenomenon is called mutual inductance. Mutual inductance is the basic operating principle of transformers, motors, and generators having the magnetic field.
In this question, we need to determine the mutual inductance between the coils for which we will use the formulae of magnetic field and of the coil which is given as \[B = \dfrac{{{\mu _0}I}}{{2R}}\]_.

Complete step by step answer: Given the radius of a small coil\[ = r\]
The radius of the large coil \[ = R\]

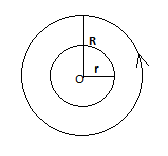
When current flows through the larger coil, it will produce a magnetic field, so the magnetic field at the center due to the larger coil of radius R will be
\[B = \dfrac{{{\mu _0}I}}{{2R}} - - (i)\], where I am the current through the coil
Now when current flows through the coil, it produces magnetic flux, which tends to flow to the smaller coil; hence the magnetic flux linkage between the two coils will be
\[\phi = B \times A\], where\[A\]is the area of the smaller loop
This can be written as
\[\phi = \dfrac{{{\mu _0}I}}{{2R}} \times \pi {r^2} - - (ii)\]
Now when this magnetic flux from the larger coil links with a smaller coil, this will induce a voltage in the smaller coil due to the larger coil, and this is known as mutual inductance, given as
 \[M = \dfrac{\phi }{i}\]
From equation (ii)
\[\dfrac{\phi }{I} = \dfrac{{{\mu _0}}}{{2R}} \times \pi {r^2} - - (iii)\]
Where \[M = \dfrac{\phi }{i}\]
Hence the mutual inductance will be
\[M = \dfrac{\phi }{I} = \dfrac{{{\mu _0}\pi {r^2}}}{{2R}} - - (iv)\]
Now from equation (iv), we can say
\[M = \dfrac{{{r^2}}}{R}\]
Option (B) is correct.

Note: Students must note that the mutual voltage in the secondary coil can be positive or the negative based on the direction of the orientation of both the coils