Question

A series R - L - C \[\left( R=10\Omega ~,{{X}_{L}}=20\Omega ,{{X}_{c}}=20\Omega \right)\] circuit is supplied by \[V=\sin \omega t\text{ Volt}\] then power dissipation in circuit is,
\[\text{A}\text{. Zero Watt}\]
\[\text{B}\text{.10 Watt}\]
\[\text{C}\text{. 5 Watt}\]
\[\text{D}\text{. 2}\text{.5 Watt}\]

Answer 1

Hint: Power dissipated in a R-L-C circuit can be expressed in terms of rms current and voltage.
When \[{{X}_{L}}={{X}_{C}}\] resonance occurs in the RLC circuit .Then the impedance of the R-L-C circuit will be equal to the value of resistance connected to that circuit.
Formula used:
\[\text{Power dissipated, P = }{{\text{i}}_{rms}}{{E}_{rms}}\cos \Phi \]
\[\tan \Phi =\dfrac{{{X}_{L}}-{{X}_{C}}}{R}\]
\[{{I}_{rms}}=\dfrac{{{I}_{o}}}{\sqrt{2}}\]
\[{{E}_{rms}}=\dfrac{{{E}_{o}}}{\sqrt{2}}\]
\[{{V}_{rms}}=\dfrac{{{V}_{o}}}{\sqrt{2}}\]
\[P=\dfrac{V_{rms}^{2}}{{{Z}^{2}}}R\]

Complete answer:
Let us draw the R-L-C diagram,

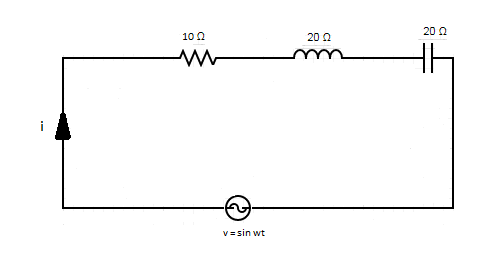
Given,
\[R=10\Omega \]
\[{{X}_{L}}=20\Omega \]
\[{{X}_{c}}=20\Omega \]
\[V=\sin \omega t\text{ Volt}\]
\[\text{Power dissipated, P = }{{\text{i}}_{rms}}{{E}_{rms}}\cos \Phi \] ------ 1
Here\[{{X}_{L}}={{X}_{c}}=20\Omega \],
Hence the impedance diagram can be drawn as
Therefore,
\[\text{Impedance, Z=R}\] ------ 2
The phase angle between the voltage and current is represented by \[\Phi \]. The tangent of this angle is given by,
\[\tan \Phi =\dfrac{{{X}_{L}}-{{X}_{C}}}{R}\]
Substitute the values of \[{{X}_{L}}\],\[{{X}_{C}}\], \[R\]
We get,
\[\tan \Phi =\dfrac{20-20}{10}=0\]
\[\Phi =0\]
Then,
\[\cos \Phi =\cos 0=1\] ------- 3
Now, we need to find the values of\[{{\text{i}}_{rms}}\text{ and }{{E}_{rms}}\].
\[{{i}_{0}}=\dfrac{{{V}_{0}}}{Z}=\dfrac{10}{R}=\dfrac{10}{10}=1A\]
Then,
\[{{\text{i}}_{rms}}\dfrac{{{I}_{o}}}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}A\] --------- 4
\[{{E}_{rms}}\dfrac{{{E}_{o}}}{\sqrt{2}}=\dfrac{10}{\sqrt{2}}V\] ----------5
Substitute equations 3, 4, and 5 in equation 1
\[\text{Power dissipated, P= }{{\text{i}}_{rms}}{{E}_{rms}}\cos \Phi \]
\[P=\dfrac{1}{\sqrt{2}}\times \dfrac{10}{\sqrt{2}}\times 1=\dfrac{10}{2}=5W\]

So, the correct answer is “Option C”.

Note:
Alternate method to solve the question.
We have power dissipation,
\[P=\dfrac{V_{rms}^{2}}{{{Z}^{2}}}R\] --------- 1
\[{{V}_{rms}}=\dfrac{{{V}_{0}}}{\sqrt{2}}=\dfrac{10}{\sqrt{2}}\] ---------- 2
Here, \[Z=R=10\] --------- 3
Substituting equation 2 and 3 in equation 1.
\[P=\dfrac{{{\left( \dfrac{10}{\sqrt{2}} \right)}^{2}}}{{{10}^{2}}}\times 10=\dfrac{500}{100}=5W\]