Question

 A rod of length is sliding such that one of its ends is always in contact with a vertical wall and its other end is always in contact with a horizontal surface. Just after the rod is released from rest, the magnitude of acceleration of end points of the rod is a and b respectively. The angular acceleration of rod at this instant will be:
A. \[\dfrac{{a + b}}{l}\]
B. $\dfrac{{\sqrt {\left| {{a^{^2}} - {b^2}} \right|} }}{l}$
C. $\dfrac{{\sqrt {{a^2} + {b^2}} }}{l}$
D. None of these

Answer 1

Hint:As the rod is released from rest, one end will move downward along the wall and the other point will move along ground, away from the wall. Using parallelogram law of vector addition, find the acceleration of the rod. Using formula $a = \alpha r$
 $a = $ liner acceleration
 r= radius or length of body which is performing rotational motion
 $\alpha = $ Angular acceleration


Complete step-by-step solution:

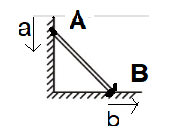
As we can see
 $
  {{\vec a}_A} = - a\hat j \\
  {{\vec a}_B} = b\hat i \\
 $
Applying parallelogram law of vector addition
\[\left| {{{\vec a}_{AB}}} \right| = \sqrt {{{\left| {{{\vec a}_A}} \right|}^2} + {{\left| {{{\vec a}_B}} \right|}^2} + 2 \times \left| {{{\vec a}_A}} \right| \times \left| {{{\vec a}_B}} \right|\cos \theta } \]
Here $\theta = {90^ \circ }$ so $\cos \theta = 0$
 \[\left| {{{\vec a}_{AB}}} \right| = \sqrt {{{\left| {{{\vec a}_A}} \right|}^2} + {{\left| {{{\vec a}_B}} \right|}^2}} \]
And we know
 $
  {{\vec a}_A} = - a\hat j \\
  {{\vec a}_B} = b\hat i \\
 $
On further putting values
 $\therefore \left| {{{\vec a}_{AB}}} \right| = \sqrt {{a^2} + {b^2}} $
Using formula $a = \alpha r$
$\therefore \left| {{{\vec a}_{AB}}} \right| = \alpha l$
$\therefore \alpha = \dfrac{{\sqrt {{a^2} + {b^2}} }}{l}$

Note:- The difference between triangular law of vector addition and parallelogram law of vector addition is that, in parallelogram law of vector addition both the vectors are placed at same origin and the resultant is the diagonal vector. Whereas, in triangle law of vector addition two vectors are in same order and the resultant is in reverse order.
In Parallelogram law of vector additionThe difference between triangular law of vector addition and parallelogram law of vector addition is that, in parallelogram law of vector addition both the vectors are placed at same origin and the resultant is the diagonal vector. Whereas, in triangle law of vector addition two vectors are in same order and the resultant is in reverse order.
In Parallelogram law of vector addition

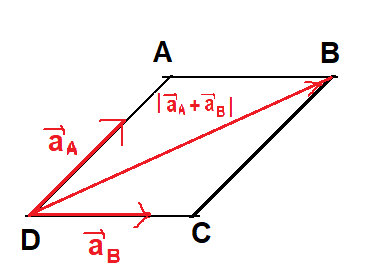
In Triangle law of vector addition