Question

A right triangle has angles which measure 30, 60 and 90 degrees. If the perimeter of this triangle is \[15 + 5\sqrt 3 \], then the length of the hypotenuse of this triangle is
A) 5
B) 7.5
C) 10
D) 12.5

Answer 1

Hint: We have been given that the triangle is a 30-60-90 degrees triangle. Here we will use the property of this type of triangle where the sides opposite to 30-60-90 degree angles are in the ratio of 1:\[\sqrt 3 \]: 2 respectively. This ratio of the sides of the 30-60-90 triangle is calculated by applying the sine rule to the triangle. The sine rule is given by\[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\], where a, b and c are sides opposite to angles A, B and C. We have also been given the perimeter so we will use the formula of perimeter to get an equation in terms of x, where x is the side opposite to 30 degrees. We can then find hypotenuse by multiplying it by 2.

Complete step by step answer:
Let us consider \[\Delta ABC\,\] to be the required 30-60-90 degree triangle.

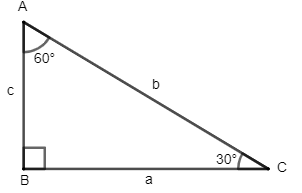
We will apply the sine rule to the given triangle.
Sine rule is given as,
\[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = k\]
Here a, b and c are the sides opposite to the angles A, B and c respectively and k is the common ratio.
Let us substitute the values of angles a, B and C in the sine rule equation.
\[\dfrac{a}{{\sin 60^\circ }} = \dfrac{b}{{\sin 90^\circ }} = \dfrac{c}{{\sin 30^\circ }} = k\]
Now we know that,
\[
  \sin 60^\circ = \dfrac{{\sqrt 3 }}{2} \\
  \sin 90^\circ = 1 \\
  \sin 30^\circ = \dfrac{1}{2} \]
Now we will substitute the values of the trigonometric sine ratios for the angles in the above equation.
\[\dfrac{a}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{b}{1} = \dfrac{c}{{\dfrac{1}{2}}} = k\]
From the above equation we get the values of the sides in terms of k.
\[
  a = \dfrac{{\sqrt 3 }}{2}k \\
  b = k \\
  c = \dfrac{1}{2}k \]
Therefore we can see that the three sides of the triangle are in a ratio as follows.
\[a:b:c = \dfrac{{\sqrt 3 }}{2}:1:\dfrac{1}{2}\]
Thus on rearranging terms, we can see that the sides of the 30-60-90 triangle are in the ratio of 1:\[\sqrt 3 \]: 2 respectively.
Since it is a 30-60-90 triangle, the sides are in the ratio 1:\[\sqrt 3 \]: 2.
We will now apply this property to find the value of the hypotenuse.
Let us assume x to be the side opposite to \[30^\circ \].
Then we get the side opposite to \[60^\circ \] as \[\sqrt 3 x\] and the side opposite to \[90^\circ \] as 2x.
 We have been given the perimeter of the triangle as \[15 + 5\sqrt 3 \].
Now let us substitute the above values in the formula of the perimeter of the triangle.
Perimeter of triangle= Sum of all sides.
\[15 + 5\sqrt 3 = x + \sqrt 3 x + 2x\]
\[\Rightarrow 15 + 5\sqrt 3 = 3x + \sqrt 3 x\]
Let us take 5 common on the L.H.S.
\[\left( {3 + \sqrt 3 } \right)5 = \left( {3 + \sqrt 3 } \right)x\]
As the term \[\left( {3 + \sqrt 3 } \right)\] cancels out we will get,
X=5.
Therefore the hypotenuse, that is side opposite to \[90^\circ \]=2x=10

So, the correct answer is “Option C”.

Note: We need to keep the solution simple and so we should directly use the ratio keeping in mind the order of the angles. Side opposite to 90 will be twice the side opposite to 30. Also, we should not use the decimal form of \[\sqrt 3 \]as it will complicate the equation. In such questions, wherever applicable we should try to get common terms on opposite sides rather than increasing the number of terms which will complicate calculation.