Question

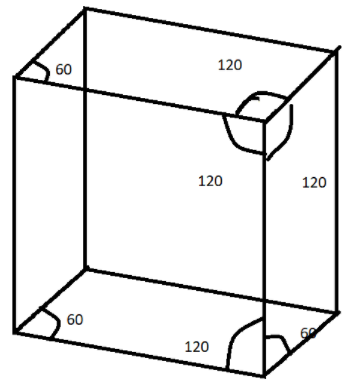
A rhombohedral unit cell is shown. What is its volume? If the side length= \[a\,{A^ \circ }\] (angstrom).
A) \[\dfrac{{{a^3}}}{{\sqrt 3 }}\]
B) \[{a^3}\dfrac{{\sqrt 3 }}{2}\]
C) \[\dfrac{{{a^3}}}{{\sqrt 2 }}\]
D) \[{a^3}\sqrt {\dfrac{3}{2}} \]

Answer 1

Hint: This question is based on trigonometry , since here we are given a rhombohedral figure and side is known and all the sides of the rhombohedral have the same length and angles are never equal to \[{90^ \circ }\], this is a simple mathematical question we just have to put the values and solve trigonometrically.
Formula Used: \[{a^3}\sqrt {1 - 3{{\cos }^2}\alpha + 2{{\cos }^3}} \alpha \], where \[\alpha \]is the angle.

Complete step-by-step solution:
According to the question, we have to find the volume of the rhombohedral. We know from the formula which is:
Volume of a rhombohedral is =\[{a^3}\sqrt {1 - 3{{\cos }^2}\alpha + 2{{\cos }^3}} \alpha \]
Where \[\alpha \]is the angle which is equivalent to \[{60^ \circ }\].
So, by substituting the values, we get:
\[Volume = {a^3}\sqrt {1 - 3{{\cos }^2}{{60}^ \circ } + 2{{\cos }^3}} {60^ \circ }\]
We also know that,
\[\Rightarrow {\operatorname{Cos} ^2}{60^ \circ } = \dfrac{1}{4}\], since \[\left[ {{{\operatorname{Cos} }^2}\theta = \dfrac{{1 + \cos 2\theta }}{2}} \right]\]
We also know that,
\[ \Rightarrow {\operatorname{Cos} ^3}{60^ \circ } = \dfrac{1}{8}\], since\[\left[ {{{\operatorname{Cos} }^3}\theta = \dfrac{{\cos {{180}^ \circ } + 3\cos {{60}^ \circ }}}{4}} \right]\]
So, now substituting the values of above written angles we get,
\[ \Rightarrow Volume = {a^3}\sqrt {1 - \dfrac{3}{4} + \dfrac{2}{8}}\]
By solving this, we get:
\[ \Rightarrow Volume = {a^3}\sqrt {1 - \dfrac{1}{2}} \]
Thus, we found out that the Volume is \[\dfrac{{{a^3}}}{{\sqrt 2 }}\].
Therefore, option C is the correct answer.

Note: The rhombohedral lattice structure has rhombohedral cells, with 3 pairs of unique rhombic faces and also remember all the sides are same and all the angles are also same but never equivalent to 90 degrees, it is the part of hexagonal crystal family.