Question

A rectangular tin sheet is 12 cm long and 5 cm board. It is rolled along its length to form a cylinder by making the opposite edges just to touch each other. Find the volume of the cylinder (in cube cm).

Answer 1

Hint: Here the length of the sheet is the height of the formed cylinder whereas the breadth is taken as the diameter of the formed cylinder, from which we will find the radius. With the help of the values of height and radius, we will find the volume of the cylinder.

Formula used:
The volume of a cylinder when its length and radius is \[h\] and \[r\] respectively, is \[V = \pi {r^2}h\].

Complete step by step solution:

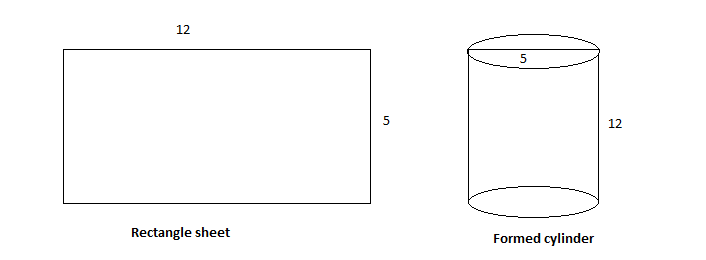
It is given that the length of the rectangular tin sheet is \[12\] cm.
The width of the rectangular tin sheet is \[5\] cm.
It is rolled along its length to form a cylinder by making the opposite edges just to touch each other.
When the rectangular tin sheet is rolled into a cylinder, the length of the rectangular sheet is equal to the height of the cylinder and the breadth will be its diameter.
So, the length of the cylinder is \[12\] cm.
And the diameter of the cylinder is \[5\] cm.
So, the radius of the cylinder is \[\dfrac{5}{2} = 2.5\] cm.
We know that, the volume of a cylinder when its length and radius is \[h\] and \[r\] respectively, is \[V = \pi {r^2}h\]
Substitute the value of length and the radius in the above equation we get,
\[V = \pi \times {2.5^2} \times 12\;c{m^3}\]
Let us take \[\pi = 3.14\] and simplify the above equation we get,
\[V = 3.14 \times 2.5 \times 2.5 \times 12\;c{m^3}\]
\[V = 235.5c{m^3}\]

Hence, the volume of the cylinder is\[235.5c{m^3}\].

Note:
We should be careful that the breadth of the rectangle sheet is converted into the radius of the cylinder and not the diameter. We can also substitute \[\pi = \dfrac{{22}}{7}\] instead of \[\pi = 3.14\] but the value of the volume will never change.