Question

A rectangular path is 45 m long and 30 m wide. A path \[2.5\] m wide is constructed outside the park. Find the area of the path.

Answer 1

Hint: Here, we need to find the area of the path. The area of the path is the difference in the areas of the two rectangles. We will use the formula for the area of a rectangle to find the two areas. Then subtract the area of the smaller rectangle from the area of the bigger rectangle to find the required area of the path.

Formula Used: We will use the formula Area of rectangle \[ = l \times b\], where \[l\] is the length of the rectangle and \[b\] is the breadth of the rectangle.

Complete step-by-step answer:
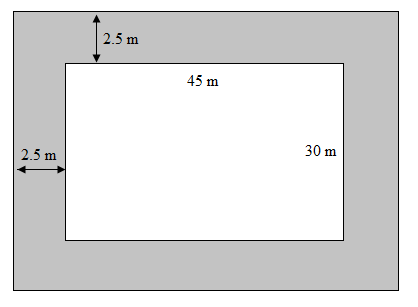
From the figure, we can observe that the area of the path is the difference in the area of the bigger rectangle and the smaller rectangle.
First, we will calculate the area of the smaller rectangle.
Substituting the length as 45 m, and the breadth as 30 m in the formula Area of rectangle \[ = l \times b\], we get
Area of the smaller rectangle \[ = 45 \times 30{\rm{ }}{{\rm{m}}^2}\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Area of the smaller rectangle \[ = 1350{\rm{ }}{{\rm{m}}^2}\]
Thus, we get the area of the smaller rectangle as 1350 square metres.
Now, we will calculate the area of the bigger rectangle.
The path is \[2.5\] m wide.
The length of the bigger rectangle is the sum of the length of the smaller rectangle, and twice the width of the path.
Thus, we get
Length of the bigger rectangle \[ = 45 + 2\left( {2.5} \right)\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Length of the bigger rectangle \[ = 45 + 5\]
Adding the terms, we get
\[ \Rightarrow \] Length of the bigger rectangle \[ = 50\] m
Similarly, the breadth of the bigger rectangle is the sum of the breadth of the smaller rectangle, and twice the width of the path.
Thus, we get
Breadth of the bigger rectangle \[ = 30 + 2\left( {2.5} \right)\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Breadth of the bigger rectangle \[ = 30 + 5\]
Adding the terms, we get
\[ \Rightarrow \] Breadth of the bigger rectangle \[ = 35\] m
Substituting the length as 50 m and the breadth as 35 m in the formula for area of a rectangle, we get
Area of the bigger rectangle \[ = 50 \times 35{\rm{ }}{{\rm{m}}^2}\]
Multiplying the terms in the expression, we get
\[ \Rightarrow \] Area of the bigger rectangle \[ = 1750{\rm{ }}{{\rm{m}}^2}\]
Thus, we get the area of the bigger rectangle as 1750 square metres.
Finally, we can calculate the area of the path.
The area of the path is the difference in the area of the bigger rectangle and the smaller rectangle.
Therefore, we get
Area of the path \[ = 1750{\rm{ }}{{\rm{m}}^2} - 1350{\rm{ }}{{\rm{m}}^2}\]
Subtracting the terms in the expression, we get
\[ \Rightarrow \] Area of the path \[ = 400{\rm{ }}{{\rm{m}}^2}\]
Therefore, we get the area of the path as 400 square metres.

Note: A common mistake is to calculate the length of the bigger rectangle as the sum of the length of the smaller rectangle, and the width of the path, that is \[45 + 2.5 = 47.5{\rm{ m}}\]. This is incorrect, because the path is constructed around all the sides of the smaller rectangle. Therefore, the length of the smaller rectangle is increased by \[2.5\] m from both left and right side to get the length of the bigger rectangle. Similarly, the breadth of the bigger rectangle is calculated.