Question

A rectangular loop of sides 10cm and 5cm carrying a current $I$ of $12A$ is placed in different orientations as shown in the figure below:
If there is a uniform magnetic field of $0.3T$ in the positive z-direction, in which orientations the loop would be in
(A) Stable equilibrium and
(B) Unstable equilibrium?

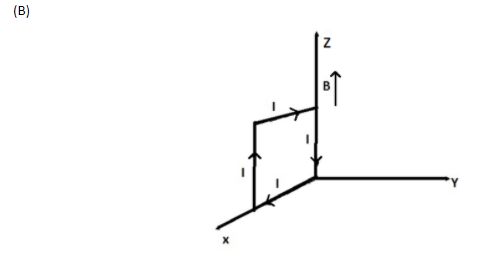
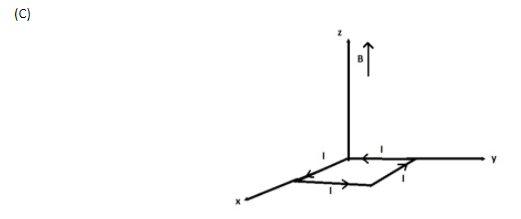
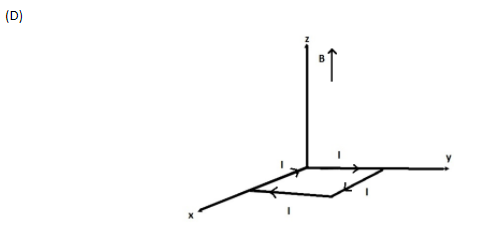
(A) (a) and (b) respectively
(B) (a) and (c) respectively
(C) (b) and (d) respectively
(D) (b) and (c) respectively

Answer 1

Hint: It has been given that the magnetic field $B$ is uniform. Only torque acts on a current carrying loop. Stable orientation has minimum energy and vice versa.
Formula Used: The formulae used in the solution are given here.
The loop carries a current $I$, has $N$ turns, each of area $A$, and the perpendicular to the loop makes an angle $\theta $ with the field $B$.
$\tau = N \cdot I \cdot ab \cdot B\sin \theta = NIAB\sin \theta $.
Magnetic moment $m = IA$.

Complete Step by Step Solution: Since the magnetic field $B$ is uniform, only torque acts on a current carrying loop.
The torque exerted on a current-carrying coil placed in a magnetic field can be given by the vector product of the magnetic moment and the magnetic field. A uniform magnetic field exerts no net force on a current loop but it does exert a net torque.
Let's say the magnetic field is in the plane of the loop and is parallel to two sides.
The loop carries a current $I$, has $N$ turns, each of area $A$, and the perpendicular to the loop makes an angle $\theta $ with the field $B$.
$\tau = N \cdot I \cdot ab \cdot B\sin \theta = NIAB\sin \theta $.
This is the torque on a current-carrying loop in a uniform magnetic field. The net force on the loop is zero.
Given that, a rectangular loop of sides 10cm and 5cm carries a current $I$of $12A$ and there is a uniform magnetic field of $0.3T$ in the positive z-direction.
Thus, ${\text{I = 12A}}$ and $B = 0.3\hat kT$ and area $A = 5 \times 10 \times {10^{ - 4}}{m^2} = 50 \times {10^{ - 4}}{m^2}$.
The magnetic moment of a current loop can be defined as the product of the current flowing in the loop and the area of the rectangular loop. Thus,
$m = IA = 12 \cdot 50 \times {10^{ - 4}} = 6 \times {10^{ - 2}}A{m^2}$.
Now, ${\vec M_1}$ has magnitude $6 \times {10^{ - 2}}A{m^2}$ and acts in the $\hat i$ direction, ${\vec M_2}$ has magnitude $6 \times {10^{ - 2}}A{m^2}$ and acts in the $\hat k$ direction, ${\vec M_3}$ has magnitude $6 \times {10^{ - 2}}A{m^2}$ and acts in the $\hat j$ direction, and ${\vec M_4}$ has magnitude $6 \times {10^{ - 2}}A{m^2}$ and acts in the $\hat k$ direction.
Potential energy is minimum for${\vec M_2}$, since it is parallel to$\vec B$, the loop is thus in equilibrium for (b).
Potential energy is maximum for ${\vec M_4}$, since it is anti-parallel to $\vec B$, the loop is thus unstable for (d).

Hence, the correct answer is Option C.

Note: We know that, $\tau = m \times B$
$ \Rightarrow \left| \tau \right| = \left| m \right|\left| B \right|\sin \theta $.
For the second orientation, that is, the one in (b), $\theta = {0^ \circ }$,
$ \Rightarrow \tau = 0$.
That is the stable orientation.
For the fourth orientation, the one in (d), $\theta = \pi $,
$ \Rightarrow \tau = 0$.
This is the unstable orientation.