Question

A rectangular lawn $ 80m \times 60m $ has two roads each $ 10 $ m wide running in the middle of it, one parallel to the length and the other parallel to the breadth. Find the cost of gravelling them at ₹. $ 1.20 $ per sq. metre.

Answer 1

Hint: To find the total cost of grazing the roads which run in the middle of rectangular lawn, both of roads are parallel to the length and breadth of the rectangular lawn. We first calculate the area of the both roads and then multiplying the total area with one square unit to get the total cost of gravelling.
Area of rectangular lawn = $ length \times breadth $ , Total cost = $ total\,\,area\,\, \times \,\cos t\,per\;unit\, $

Complete step-by-step answer:

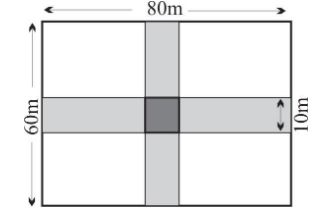
Dimension of the rectangular lawn is $ 80m \times 60m $ .
Length of rectangular lawn is $ 80m $ .
Breadth of rectangular lawn is $ 60m. $
Width of the roads which runs parallel to length and breadth
 of rectangular lawn is $ 10m. $
As, one road is parallel to the length of a rectangular lawn. Therefore its length will also be equal to the length of the rectangular lawn.
 $ \therefore $ Length of road which is parallel to length of rectangular lawn = $ 80m. $
Area of the road which is $ 80m $ long and $ 10m $ wide is given as: $ length \times breadth $
$\Rightarrow$ Area of one road which is parallel to length of the rectangular lawn is = $ 80 \times 10 $
Area of one road = $ 800{m^2} $
Also, another road is parallel to the breadth of a rectangular lawn. Therefore its length will also be equal to the breadth of the rectangular lawn.
 $ \therefore $ Length of the second road which is parallel to breadth of the rectangular lawn = $ 60m $ .
Area of the road which is $ 60m $ long and $ 10m $ wide is given as: $ length \times breadth $
$\Rightarrow$ Area of second road which is parallel to breadth of the rectangular lawn is $ = 60 \times 10 $
Area of second road $ = 600{m^2} $
Therefore total area of the both roads is given as = area of 1st road + area of 2nd road
Area of roads = $ 800 + 600 = 1400 $
Total area of both roads is $ 1400{m^2} $
From the figure we see that the square portion that formed in the middle of the intersection of the road is considered twice. Therefore we subtract the area of the square portion from the total area of roads that we calculated above.
Side of square formed in middle is = with of the road = $ 10m $
$\Rightarrow$ Area of square formed in middle is = $ {(side)^2} $
$\Rightarrow$ Area of square formed in middle = $ {\left( {10} \right)^2} $
$\Rightarrow$ Area of square formed in middle = $ 100{m^2} $
$\Rightarrow$ Actual area of roads = total area of roads – area of square formed in middle of roads.
$\Rightarrow$ Actual area of roads = $ 1400 - 100 $
$\Rightarrow$ Actual area of roads = $ 1300{m^2} $
Cost of gravelling per square metre =₹. $ 1.20 $
Total cost of gravelling roads = Total area of roads $ \times $ cost per square metre
Therefore total cost of gravelling roads = $ 1300 \times 1.20 $
$\Rightarrow$ Cost of gravelling roads = ₹. $ 1560 $
Hence, from above we see that total cost of gravelling roads which runs parallel to length and breadth of width $ 10m $ is ₹. $ 1560 $

Note: While doing this type of problem students must be careful regarding that square formed in the middle of two roads. As students, while calculating the total area of roads just add the area of two roads after calculating them as individuals, which leads to wrong answers. Because, they took an area of square that formed at the intersection of two roads two times.