Question

A rectangle has dimensions $40m\times 25m$. If the length and breadth are increased by 15%, find the percentage increases in its area.

Answer 1

Hint: We describe the relation between the sides of a rectangle and its area. We increase the length of the sides following the percentage increase. We find the change in areas and find its percentage.

Complete step by step solution:
It is given that the dimensions of the rectangle is $40m\times 25m$ which means length is $40m$ and breadth is $25m$.
The area of the rectangle was $40\times 25=1000{{m}^{2}}$.

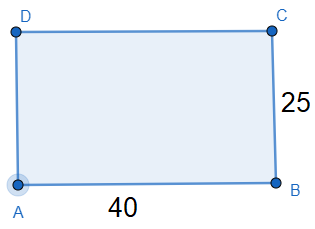
Now we have increased the length and breadth by 15%.
For the given percentage 15% of 40 and 15% of 25, we first need to find the mathematical form.
We know for any arbitrary percentage value of a%, we can write it as $\dfrac{a}{100}$. The percentage is to find the respective value out of 100. The increased value for the main number $x$ becomes $x+\dfrac{ax}{100}=x\left( 1+\dfrac{a}{100} \right)$.
Therefore, 15% increase on 25 can be written as $25\left( 1+\dfrac{15}{100} \right)=\dfrac{25\times 115}{100}=28.75$.
Therefore, 15% increase on 40 can be written as $40\left( 1+\dfrac{15}{100} \right)=\dfrac{40\times 115}{100}=46$.
The length and the breadth of the new rectangle becomes $46m\times 28.75m$.
The area of the new rectangle was $46\times 28.75=1322.5{{m}^{2}}$.
The increase in the area is $1322.5-1000=322.5{{m}^{2}}$.
The percentage increase will be $\dfrac{322.5}{1000}\times 100=32.25$.

Therefore, the percentage increase in the rectangle’s area is $32.25$

Note: The value of the fraction is actually the unitary value of 15 out of 100. Therefore, in percentage value we got $32.25$ as the percentage. Percentage deals with the ratio out of 100. The ratio value for both fraction and percentage is the same.