Question

A ray of light strikes a glass plate at an angle $60^\circ$ if the reflected and refracted waves are perpendicular to each other, the index of refraction of glass is

Answer 1

Hint: Recall that the ray of light bends when it travels from one medium to another medium. The degree to which the ray of light bends in the medium is described by Snell’s law of refraction. It shows the relation between angle of incidence and refraction and the refractive index for a pair of mediums.

Complete step by step answer:
Step I:
According to Snell’s law the ratio of sine of angle of incidence and the sine of angle of refraction is constant for a given pair of mediums.
$\dfrac{{\sin i}}{{\sin r}} = \mu $
Where $i $ is the angle of incidence, $r $ is the angle of refraction, and $\mu $ is a constant.
Also the refracted ray, the incident ray and the normal all lie in the same plane.
Given that the ray of light strikes a glass plate at an angle of ${60^\circ }$with the surface of the glass. Also if the reflected and the refracted waves are perpendicular to each other then

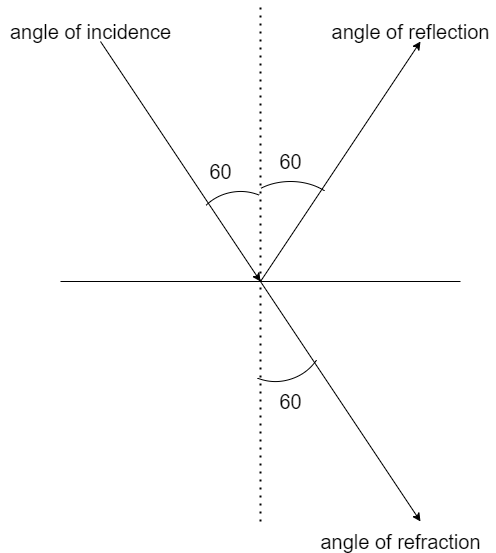
If the reflected light is polarised then the angle between reflected and refracted ray will be ${90^\circ }$
The angle of refraction $30^\circ $
And the angle of incidence $60^\circ $
Step II:
The refractive index of the glass is given as
$\mu = \dfrac{{\sin i}}{{\sin r}}$
$\Rightarrow \mu = \dfrac{{\sin {{60}^\circ }}}{{\sin {{30}^\circ }}}$
$\Rightarrow \mu = \dfrac{{\dfrac{{\sqrt 3 }}{2}}}{{\dfrac{1}{2}}}$
$\Rightarrow \mu = \sqrt 3 $
$\Rightarrow \mu = 1.732$

Therefore the refractive index of the glass will be $1.732$.

Note:
It is to be noted that the Snell’s law of refraction, shows that the ray of light when travels from one medium to another will deviate towards the normal in the optically denser medium and away from the normal in the optically rarer medium. So, the refractive index of denser medium will be high and that of the optically rarer medium will be low.