Question

A railway train is travelling on a curve of 750m radius at 30km/hr through to what angle it turns in 10 second.

Answer 1

Hint:
First of all we’ll use the distance formula which is Distance formula \[ = Speed \times Time\], to get the distance travelled by train in 10 seconds. And then by using formula arc length formula; \[\theta = \dfrac{{arc{\text{ }}length}}{{radius}} = \dfrac{l}{r}\], we’ll get the required answer. In the above mentioned formula l represents arc length, r represents the radius of the circle and \[\theta \] represents the angle in radians made by the arc at the centre of the circle.

Complete step by step solution:

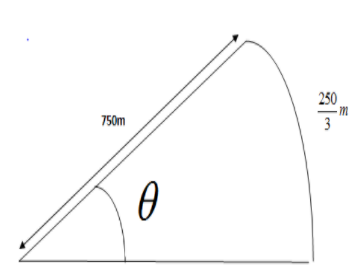
Given: Radius of the curve =750 m.
Speed at the railway train in travelling =30km/hr
\[
   = \dfrac{{30 \times 1000}}{{3600}}m/s \\
   = \dfrac{{30 \times 5}}{{18}}m/s \\
   = \dfrac{{150}}{{18}}m/s \\
 \]
Distance travelled by the train in 10 second;
\[ = Dis\tan ce = Speed \times Time\]
\[
   = Dis\tan ce = Speed \times Time \\
   \Rightarrow Dis\tan ce = \dfrac{{150}}{{18}} \times 10m \\
   \Rightarrow Dis\tan ce = \dfrac{{250}}{3}m \\
 \]
Now, using Arc length formula; \[\theta = \dfrac{{arc{\text{ }}length}}{{radius}}\]
\[
   \Rightarrow \theta = \dfrac{{\dfrac{{250}}{3}}}{{750}}radian \\
   \Rightarrow \theta = \dfrac{{250}}{3} \times \dfrac{1}{{750}}radian \\
   \Rightarrow \theta = \dfrac{1}{9}radian \\
 \]

The train will make an angle of \[\dfrac{1}{9}radian\].

Note:
This is a classic problem connecting our real life to mathematics. In higher studies, the same question can be asked with a slight change. They’ll give a certain condition and say the train is running on the path which follows this condition. We have to find the path of the train. This kind of problem can be solved by locus concept.