Question

A projectile is launched from point O at an angle of ${22}^{\circ}$ with an initial velocity of $15 ms^{-1}$ up an inclined plane that makes an angle of ${10}^{\circ}$with the horizontal. The projectile hits the inclined plane at point M. Find the distance OM.
A. 10 m
B. 15 m
C. 20 m
D. 25 m

Answer 1

Hint: This question is based on the concept of the projectile motion. We will make use of the components of the displacement which involves the velocity of the motion, the time is taken, the angle made by the projectile, and the gravitational constant to find the value of the time taken. Then, using the given values of the angles and the time taken to find the value of the distance.
Formula used:
\[x={{V}_{0}}\cos (\theta )t\]
\[y={{V}_{0}}\sin (\theta )t-\left( \dfrac{1}{2} \right)g{{t}^{2}}\]

Complete step-by-step solution
The diagram representing the projectile motion of the projectile is as follows.

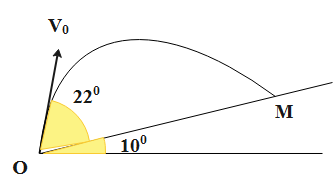
Firstly, let us go through the formulae of the components of the displacement in the case of a projectile.
The x component of the displacement is given as follows.
\[x={{V}_{0}}\cos (\theta )t\]
Where \[{{V}_{0}}\]is the velocity of the motion, t is the time taken and\[\theta \] is the angle made by the projectile.
The y component of the displacement is given as follows.
\[y={{V}_{0}}\sin (\theta )t-\left( \dfrac{1}{2} \right)g{{t}^{2}}\]
Where \[{{V}_{0}}\]is the velocity of the motion, t is the time taken, \[\theta \] is the angle made by the projectile and g is the gravitational constant.
From the data, we have the data as follows.
The angle made by the projectile, \[\theta =22+10=32{}^\circ \]
The velocity of the motion, \[{{V}_{0}}=15{m}/{s}\;\]
The relationship between the coordinates x and y with the inclination is given as follows.
\[\tan 10{}^\circ =\dfrac{y}{x}\]
Now, let us substitute the given values in the formulae mentioned above.
\[\tan 10{}^\circ =\dfrac{{{V}_{0}}\sin (\theta )t-\left( \dfrac{1}{2} \right)g{{t}^{2}}}{{{V}_{0}}\cos (\theta )t}\]
Continue the further calculation.
\[\left( \dfrac{1}{2} \right)gt+{{V}_{0}}\cos (\theta )\tan 10{}^\circ -{{V}_{0}}\sin (\theta )=0\]
Substitute the given values and solve the above equation to obtain the value of time taken.
\[\begin{align}
  & t=\dfrac{{{V}_{0}}\sin (\theta )-{{V}_{0}}\cos (\theta )\tan 10{}^\circ }{0.5g} \\
 & t=\dfrac{{{V}_{0}}\sin 32{}^\circ -{{V}_{0}}\cos 32{}^\circ \tan 10{}^\circ }{0.5\times 9.8} \\
 & t=1.16s \\
\end{align}\]
Therefore, the time taken is 1.16 s.
Now, we will find the distance OM.
From the figure, it’s clear that the distance OM is given as follows.
\[OM=\sqrt{\left[ {{\left( {{V}_{0}}\cos (\theta )t \right)}^{2}}+{{({{V}_{0}}\sin (\theta )t-\left( {}^{1}/{}_{2} \right)gt)}^{2}} \right]}\]
Substitute the given values and solve the above equation to obtain the value of distance OM.
\[\begin{align}
  & OM=\sqrt{\left[ {{\left( 15\times \cos 32{}^\circ \times 1.16 \right)}^{2}}+{{(15\times \sin 32{}^\circ \times 1.16-\left( {}^{1}/{}_{2} \right)\times 9.8\times 1.16)}^{2}} \right]} \\
 & OM=15\,m \\
\end{align}\]
\[\therefore \] The value of the distance OM is 15 m.
As the value of the distance, OM is 15 m, thus, option (B) is correct.

Note: This question is a direct one. The units of the parameters should be taken care of. The formulae for computing the components of the displacement in the case of a projectile should be known to solve such problems. Here x, y represent the x-coordinate and y-coordinates respectively for the projectile at an angle $32^{\circ}$ with the horizontal axis.