Question

A polygon has interior angles of \[162{}^\circ \]. How many sides does it have?

Answer 1

Hint: This question is from the topic of geometry. In solving this question, we will first know about the supplementary angles. After that, we will write the sum of all interior angles and all exterior angles and make that sum equal to n times of 180 degrees. After that, we will solve the further question. After that, we will get our answer.

Complete step-by-step solution:
Let us solve this question.
In this question, we have given that a polygon has an interior angle of \[162{}^\circ \]. We have to find the side in that polygon.
Let us take reference from the following figure.

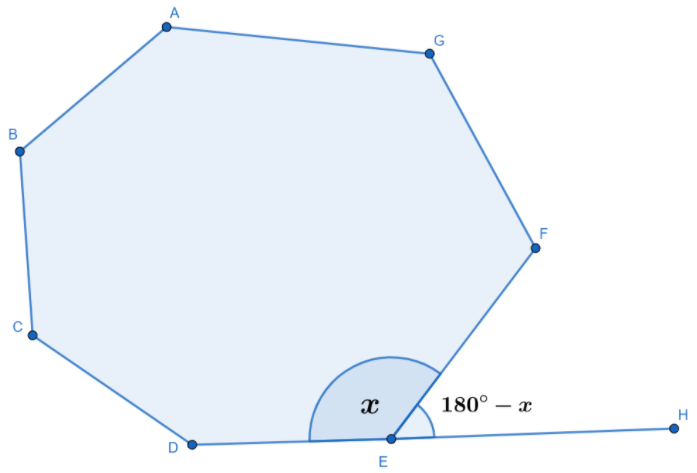
Suppose, the above polygon has n sides
We can see that angle FED and angle FEH are supplementary angles because their sum is 180 degrees. Here, we can say that angle FED is an interior angle and FEH is exterior angle. Similarly, all points have interior and exterior angles and we know that the sum of interior angle and exterior angle is 180 degrees. So, we can write
\[\text{Sum of all interior angles + Sum of all exterior angles = n}\times \text{180}{}^\circ \]
If we add all exterior angles, then it will be \[360{}^\circ \], so we can write
\[\Rightarrow \text{Sum of all interior angles + }360{}^\circ \text{ = n}\times \text{180}{}^\circ \]
The above can also be written as
\[\Rightarrow \text{Sum of all interior angles = n}\times \text{180}{}^\circ -\text{ }360{}^\circ \text{ }=\text{n}\times \text{180}{}^\circ -\text{ 2}\times \text{180}{}^\circ \text{ = 180}{}^\circ \left( \text{n-2} \right)\]
There is an n-sided polygon and we know that each side of a polygon is equal to the other, each angle of a polygon is equal to the other and if it is n-sided, then it will have n interior angles. So, we can write
\[\Rightarrow \text{n}\times \text{ interior angle = 180}{}^\circ \left( \text{n-2} \right)\]
So, we get that
\[\Rightarrow \text{ interior angle =}\dfrac{\text{ 180}{}^\circ }{\text{n}}\left( \text{n-2} \right)\]
So, we have given interior angle as \[162{}^\circ \]. Hence, we can write
\[\Rightarrow \text{ }162{}^\circ \text{ =}\dfrac{\text{ 180}{}^\circ }{\text{n}}\left( \text{n-2} \right)\]
\[\Rightarrow \text{ }\dfrac{162{}^\circ }{\text{180}{}^\circ }\text{=}\dfrac{\left( \text{n-2} \right)}{\text{n}}\]
\[\Rightarrow \text{ }\dfrac{9}{10}\text{=}\dfrac{\left( \text{n-2} \right)}{\text{n}}\]
The above can also be written as
\[\Rightarrow 9\text{n=}10\left( \text{n-2} \right)\]
\[\Rightarrow 9n=10n-20\]
Hence, we get that
\[\Rightarrow n=20\]
So, the sides of the polygon is 20 whose interior angle is \[162{}^\circ \].

Note: As we can see that this question is from the topic geometry, so we should have a better knowledge in that topic. We should remember the following formula of interior angle of any polygon:
\[\text{interior angle =}\dfrac{\text{ 180}{}^\circ }{\text{n}}\left( \text{n-2} \right)\], where n is the total number of sides of polygon.
Remember that in every polygon, the sum of all exterior angles is 360 degrees.
And, we should know about supplementary angles. The sum of supplementary angles is always 180 degrees. We can take reference from the following:

Hence, angle \[x\] and \[\text{180}{}^\circ -x\] are supplementary angles.