Question

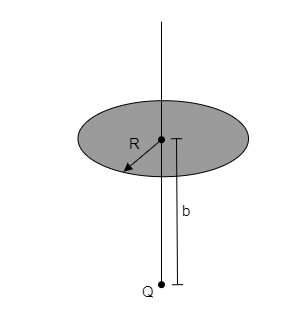
A point charge $Q$ is located on the axis of a disc of a radius $R$ at a distance $b$ from the plane of the disc (figure). Show that if one-fourth of the electric flux from the charge passes through the disc, then $R = \sqrt 3 b$

Answer 1

Hint: Electric flux can be described as the strength of the electric field in a given surface. Gauss’ law gives the electric flux through a given surface as $\dfrac{1}{{{\varepsilon _0}}}$ times that of the charge enclosed by that surface. However, the given disc is said to enclose only one-fourth of this charge.

Formulas used:
->The electric flux through a surface element is given by, $d\phi = E \cdot ds$ where $E$ is the electric field and ${\text{ds}}$ is the elemental area.
->The electric field at a distance $r$ from a charge $q$ is given by, $E = \dfrac{q}{{4\pi {\varepsilon _0}{r^2}}}$ where ${\varepsilon _0}$ is the permittivity of the free space

Complete step-by-step solution:
->Step 1: Sketch the charge located at the axis of the disc and consider an elemental area of the disc.

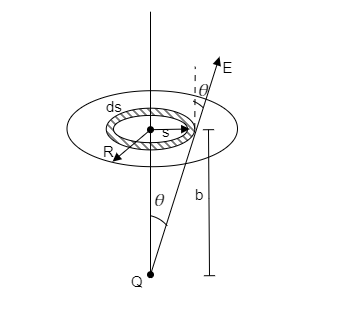
In the above figure, we consider an elemental area of the disc to be an annual ring of radius $s$ and width $ds$. Let $dA = 2\pi sds$ be the area of this element.
We see that the electric field is directed at an angle $\theta $ with the normal of the ring. However, it has the same magnitude at every point on the ring and it is given by, ${E_{ring}} = \dfrac{Q}{{4\pi {\varepsilon _0}\left( {{s^2} + {b^2}} \right)}}$
It is given that the electric flux passing through the disc is ${\phi _{disc}} = \dfrac{Q}{{4{\varepsilon _0}}}$
->Step 2: Obtain an expression for the electric flux through the ring.
The electric flux through the elemental area will be $d{\phi _{ring}} = {E_{ring}}dA\cos \theta $ ----- (1)
From the figure we have $\cos \theta = \dfrac{b}{{\sqrt {{s^2} + {b^2}} }}$
Substituting for ${E_{ring}} = \dfrac{Q}{{4\pi {\varepsilon _0}\left( {{s^2} + {b^2}} \right)}}$ , $dA = 2\pi sds$ and $\cos \theta = \dfrac{b}{{\sqrt {{s^2} + {b^2}} }}$ in equation (1) we get, $d{\phi _{ring}} = \dfrac{{Qb2\pi sds}}{{4\pi {\varepsilon _0}{{\left( {{s^2} + {b^2}} \right)}^{3/2}}}}$ ------- (2)
Step 3: Integrate equation (2) to obtain the electric flux through the disc.
The electric flux through the disc is expressed as ${\phi _{disc}} = \int\limits_0^R {d{\phi _{ring}}} $ --------- (3)
Substituting equation (2) in (3) we get, ${\phi _{disc}} = \int\limits_0^R {\dfrac{{Qb2\pi sds}}{{4\pi {\varepsilon _0}{{\left( {{s^2} + {b^2}} \right)}^{3/2}}}}} = \dfrac{{Qb}}{{2{\varepsilon _0}}}\int\limits_0^R {\dfrac{{sds}}{{{{\left( {{s^2} + {b^2}} \right)}^{3/2}}}}} = \dfrac{{Qb}}{{2{\varepsilon _0}}}\left[ {\dfrac{1}{{\sqrt {{s^2} + {b^2}} }}} \right]_0^R$
On applying the limits we have ${\phi _{disc}} = \dfrac{{Qb}}{{2{\varepsilon _0}}}\left[ {\dfrac{1}{b} - \dfrac{1}{{\sqrt {{R^2} + {b^2}} }}} \right]$
We thus have ${\phi _{disc}} = \dfrac{Q}{{2{\varepsilon _0}}}\left[ {1 - \dfrac{b}{{\sqrt {{R^2} + {b^2}} }}} \right] = \dfrac{Q}{{4{\varepsilon _0}}}$
Cancelling out the similar terms on both sides and simplifying the above equation we get, $\dfrac{b}{{\sqrt {{R^2} + {b^2}} }} = \dfrac{1}{2}$
On squaring we get, $\dfrac{{{b^2}}}{{{R^2} + {b^2}}} = \dfrac{1}{4}$
$ \Rightarrow 3{b^2} = {R^2}$ or $R = \sqrt 3 b$ .
Hence proved.

Note:- The electric flux refers to the amount of electric field lines passing through a surface. The annual ring represents an elemental area of the disc and not the gaussian surface. The Gaussian surface of the above disc will be a sphere with the charge located at its centre. The integration limits are taken from $0$ to $R$ because the flux has to be determined for the entire area of the disc.